We place queens one row at a time keeping track of columns, main diagonals, and sub-diagonals under attack. For each row we place the queen on a column if (row, column) is not already under attack — horizontally, vertically, or diagonally. For some row, if we cannot find a non-attacked column, we backtrack.
Main diagonals are characterized by and sub-diagonals are characterized by
.
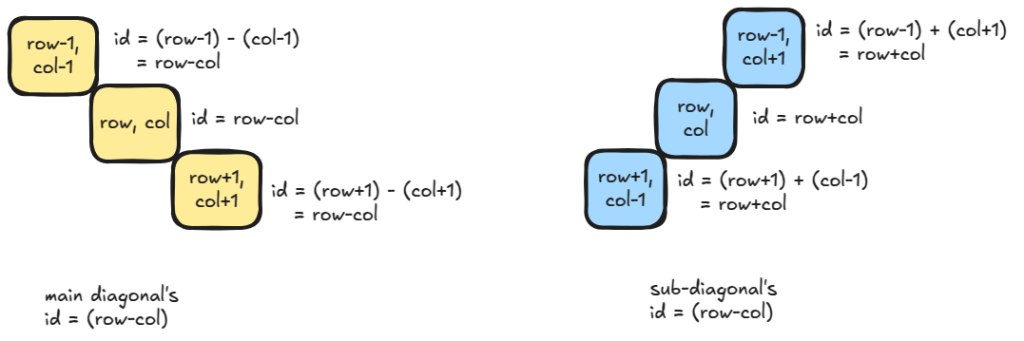
Time: , space:
.
class Solution:
def create_board_with_queens(self, n, queen_columns) -> List[str]:
board = []
for q_col in queen_columns:
row = ["."] * n
row[q_col] = "Q"
board.append("".join(row))
return board
def place_queen_on_row(
self,
n: int,
row: int,
attacked_col: Set[int],
attacked_main_diag: Set[int],
attacked_sub_diag: Set[int],
queen_columns: List[int],
all_placements: List[List[str]],
) -> None:
if len(queen_columns) == n:
board = self.create_board_with_queens(n, queen_columns)
all_placements.append(board)
return
for col in range(n):
if col in attacked_col:
continue
if (main_d := row - col) in attacked_main_diag:
continue
if (sub_d := row + col) in attacked_sub_diag:
continue
queen_columns.append(col)
attacked_col.add(col)
attacked_main_diag.add(main_d)
attacked_sub_diag.add(sub_d)
self.place_queen_on_row(
n,
row + 1,
attacked_col,
attacked_main_diag,
attacked_sub_diag,
queen_columns,
all_placements,
)
queen_columns.pop()
attacked_col.remove(col)
attacked_main_diag.remove(main_d)
attacked_sub_diag.remove(sub_d)
def solveNQueens(self, n: int) -> List[List[str]]:
all_placements = []
self.place_queen_on_row(
n=n,
row=0,
attacked_col=set(),
attacked_main_diag=set(),
attacked_sub_diag=set(),
queen_columns=[],
all_placements=all_placements,
)
return all_placements
We could maintain the stack ourselves. The top of the stack is the next square to consider. When we push top, we do not yet know if top has valid row or col or if it is an already attacked square; it is either (row+1, 0) or (row, col+1).
class Solution:
def create_board_with_queens(self, n: int, queen_columns: List[int]) -> List[str]:
board = []
for qcol in queen_columns:
row = ["."] * n
row[qcol] = "Q"
board.append("".join(row))
return board
def track_square(
self,
row: int,
col: int,
queen_columns: List[int],
attacked_col: Set[int],
attacked_main_diag: Set[int],
attacked_sub_diag: Set[int],
) -> None:
queen_columns.append(col)
attacked_col.add(col)
attacked_main_diag.add(row - col)
attacked_sub_diag.add(row + col)
def untrack_square(
self,
row: int,
col: int,
queen_columns: List[int],
attacked_col: Set[int],
attacked_main_diag: Set[int],
attacked_sub_diag: Set[int],
) -> None:
queen_columns.pop()
attacked_col.remove(col)
attacked_main_diag.remove(row - col)
attacked_sub_diag.remove(row + col)
def is_attacked(
self,
row: int,
col: int,
attacked_col: Set[int],
attacked_main_diag: Set[int],
attacked_sub_diag: Set[int],
) -> bool:
return (
col in attacked_col
or (row - col in attacked_main_diag)
or (row + col in attacked_sub_diag)
)
def solveNQueens(self, n: int) -> List[List[str]]:
all_placements = []
attacked_col, attacked_main_diag, attacked_sub_diag = set(), set(), set()
queen_columns = []
stack = [(0, 0)]
while stack:
top_row, top_col = stack.pop()
if top_row == n:
all_placements.append(self.create_board_with_queens(n, queen_columns))
last_row, last_col = stack.pop()
self.untrack_square(
last_row,
last_col,
queen_columns,
attacked_col,
attacked_main_diag,
attacked_sub_diag,
)
stack.append((last_row, last_col + 1))
continue
if top_col == n:
if stack:
last_row, last_col = stack.pop()
self.untrack_square(
last_row,
last_col,
queen_columns,
attacked_col,
attacked_main_diag,
attacked_sub_diag,
)
stack.append((last_row, last_col + 1))
continue
if self.is_attacked(
top_row, top_col, attacked_col, attacked_main_diag, attacked_sub_diag
):
stack.append((top_row, top_col + 1))
continue
# top is Ok.
stack.append((top_row, top_col))
self.track_square(
top_row,
top_col,
queen_columns,
attacked_col,
attacked_main_diag,
attacked_sub_diag,
)
# Next square to consider
stack.append((top_row + 1, 0))
return all_placements
Leave a comment