LeetCode 338: Counting Bits

Inspect binary representation

Count 1’s in binary representation for each index.

For a number $n$ , count_ones take $\lg{n}$ time. So, the time taken to count ones for all the numbers is the sum: $\lg{n} + \lg{(n-1)} + \ldots + \lg{2} + \lg{1}$ or time is $\lg{(n \cdot (n-1) \cdots 2 \cdot 1)} = \lg{n!}$ . We use Sterling’s approximation: $n! \approx \sqrt{2\pi n} (\frac{n}{e})^n$ . So, $\mathcal{O}(\lg{n!}) = \mathcal{O}(n \cdot \lg{n})$ .

Time: $\mathcal{O}(n \cdot \lg{n})$ , extra space (disregarding output): $\mathcal{O}(1)$ .

class Solution:
    def countBits(self, n: int) -> List[int]:
        def count_ones(x: int) -> int:
            one_count = 0
            while x > 0:
                q, r = divmod(x, 2)
                one_count += (1 if r == 1 else 0)
                x = q
            return one_count

        ans = [0] * (n+1)
        for x in range(n+1):
            ans[x] = count_ones(x) 
        return ans

Dynamic programming

On every power-of-two, an extra one-bit is added and the count-of-ones pattern restarts, as if we are counting from 0 again.

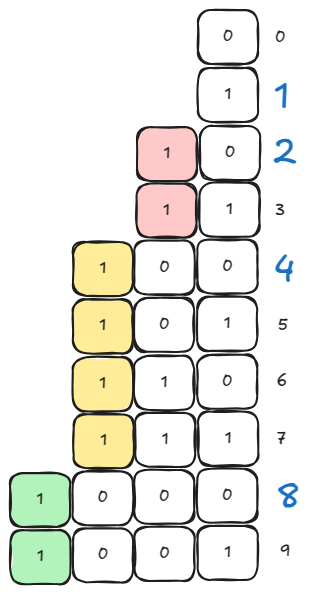
As a result, to compute count of ones in $x$ , we can use count of ones of smaller numbers. We can use Dynamic Programming.

Sub-problem

Let $C(i)$ be the count of ones in the number $i$ . Then:

$C(i) = \begin{cases} 0, & \text{if } i = 0 \\ 1 + \left\{ C\left( i-2^m \right) : 2^m \le i < 2^{m+1} \right\}, & \text{otherwise} \end{cases}$

Order

A sub-problem depends on exactly one sub-problem involving a smaller number. So, we compute count of ones in increasing order of $i$ to have a topologically sorted order of sub-problems.

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(1)$ .

class Solution:
    def countBits(self, n: int) -> List[int]:
        ans = [0] * (n+1)
        curr_pow, next_pow = None, 1
        for i in range(1, n+1):
            if i == next_pow:
                curr_pow = next_pow
                next_pow <<= 1
            ans[i] = 1 + ans[ i-curr_pow ]
        return ans

unreasonably effective