LeetCode 152: Maximum Product Subarray

Brute force

Take max of all possible subarrays.

Products of all possible subarrays starting at a particular index can be computed in $\mathcal{O}(n)$ time. Since there are $n$ possible starting indices, total time: $\mathcal{O}(n^2)$ , space: $\mathcal{O}(1)$ .

class Solution:
    def maxProduct(self, nums):
        n = len(nums)
        largest_product = float('-inf')
        for start in range(n):
            current_product = 1
            for end in range(start, n):
                current_product *= nums[end]
                largest_product = max(
                    largest_product,
                    current_product
                )
        return largest_product

Dynamic programming

Subproblem

Without negative numbers

Let $L(i)$ be the largest product in nums[0:i+1] for a subarray that includes nums[i]. Then, either nums[i] belongs to the subarray of $L(i-1)$ or nums[i]is the first element of a subarray.

$L(i) = \begin{cases} max\left( \{ L(i-1) \cdot \texttt{nums}[i], \ \texttt{nums}[i] \} \right), & \texttt{if } i > 0 \\ \texttt{nums}[i] & \texttt{otherwise} \end{cases}$

Our solution is then $\max\left( \{L(i) : 0 \le i \le n-1\} \right)$ . Because, say subarray nums[i:j+1] has the largest product. When we computed $L(i)$ , nums[i] must have started a new subarray. And $L(i+1), L(i+2), \ldots, L(j)$ all have been able to extend that subarray. So, $L(j)$ must have the product of nums[i:j+1].

With negative numbers

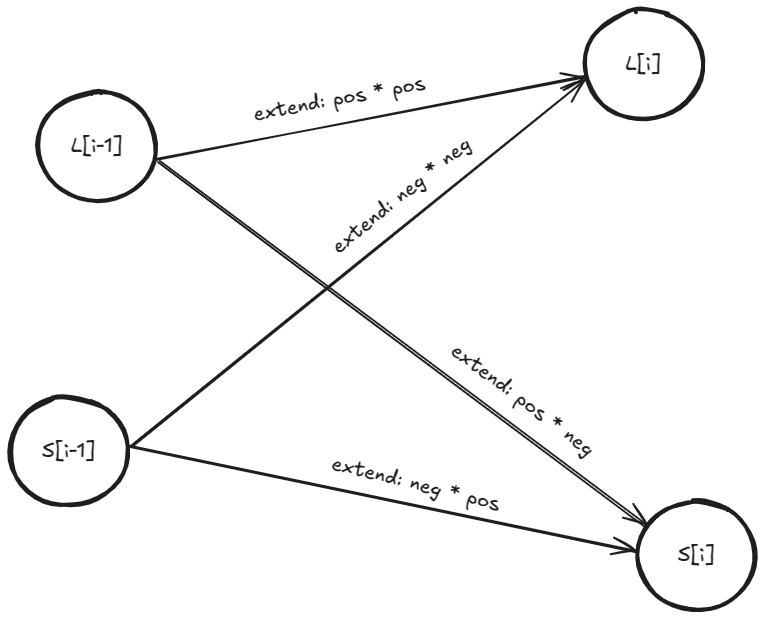
Product of two negative numbers is positive. That adds another way for nums[i] to be a part of an earlier subarray. Let $S(i)$ be the smallest product in nums[0:i+1] for a subarray that includes nums[i]. Now, we can update $L(i)$ to include negative-negative-gives-positive path:

$L(i) = \begin{cases} \max\left( \{ L(i-1) \cdot \texttt{nums}[i], \ S(i-1) \cdot \texttt{nums}[i], \ \texttt{nums}[i] \} \right), & \texttt{if } i > 0 \\ \texttt{nums}[i] & \texttt{otherwise} \end{cases}$

Symmetrically, for $S(i)$ , we include two extension paths: negative-times-positive and positive-times-negative:

$S(i) = \begin{cases} \min\left( \{ S(i-1) \cdot \texttt{nums}[i], \ L(i-1) \cdot \texttt{nums}[i], \ \texttt{nums}[i] \} \right), & \texttt{if } i > 0 \\ \texttt{nums}[i] & \texttt{otherwise} \end{cases}$

Again, we find the solution as $\max\left( \{L(i) : 0 \le i \le n-1\} \right)$ .

Order

Since edges always go from smaller indices to larger indices, we can process the numbers from left-to-right and have a topological ordering.

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(n)$ .

class Solution:
    def maxProduct(self, nums):
        n = len(nums)
        L, S = [0] * n, [0] * n
        L[0], S[0] = nums[0], nums[0]
        for i in range(1, n):
            L[i] = max(
                L[i-1] * nums[i],
                S[i-1] * nums[i],
                nums[i]
            )
            S[i] = min(
                L[i-1] * nums[i],
                S[i-1] * nums[i],
                nums[i]
            )
        
        return max(L)

Since edges always go from index i+1 to index i, we can use a single variable instead of n-sized list.

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(1)$ .

class Solution:
    def maxProduct(self, nums):
        n = len(nums)
        L, S, global_L = nums[0], nums[0], nums[0]
        for i in range(1, n):
            L, S = max(L * nums[i], S * nums[i], nums[i]), min(
                L * nums[i], S * nums[i], nums[i]
            )
            global_L = max(global_L, L)
        return global_L

unreasonably effective