LeetCode 140: Word Break II

Backtrack

If a prefix s[0:l] is a dictionary word, we then try breaking s[l:].

Time: $\mathcal{O}(n \cdot 2^n)$ , space (disregarding output-size): $\mathcal{O}(n)$ .

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:
        dict_words = set(wordDict)
        curr_words = []
        sentences = []
        def build(s):
            nonlocal dict_words, curr_words, sentences
            if not s:
                sentences.append( " ".join(curr_words) )
                return
            
            for l in range(1, len(s)+1):
                if (pref := s[0:l]) not in dict_words:
                    continue
                curr_words.append(pref)
                build(s[l:])
                curr_words.pop()
        
        build(s)
        return sentences

The solutions can be thought of as paths in a DAG.

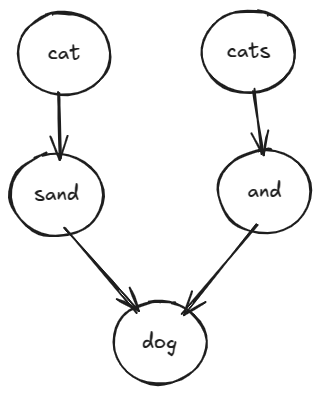
If we can construct the DAG, we can traverse the paths and collect the sentences.

Dynamic Programming

Subproblem

Say the input string is $x[1 \ldots n]$ . Let $W(i)$ be solution to the subproblem: Can we break the prefix $x[1 \ldots i]$ into dictionary words?

$W[i] = \begin{cases} \texttt{true}, & \text{if } i = 0 \\ \bigvee\left( \left\{ W(j) \wedge x[j+1 \ldots i] \in \texttt{wordDict} \right\} \right) & \text{otherwise} \end{cases}$

$W(n)$ tells us if we can break the entire input $x[1 \ldots n]$ into dictionary words.

We can piggyback on this problem to build the adjacency list of the DAG.

Order

Processing input left-to-right gives a topological ordering of the subproblems.

We have two options for building the adjacency list of the DAG:

Edge is like $j \rightarrow i$ . This means root is the subproblem $W(0)$ .
Edge is like $j \leftarrow i$ . This means root is the subproblem $W(n)$ .

If there are many false breaks in the beginning, meaning we have been able to break a prefix but did not find further break, option (2) could be better. In option (2) we would traverse only the paths that represent successful break of the entire input.

The code for the two options are almost the same except:

Edge is reversed in adj_list
Source and target of dfs are reversed: (0, n) or (n, 0).
To build the current path, we either append or appendleft.

W(0) as root

Complexity

The time complexity depends on the possible number of distinct paths in the DAG. Edges flow from an earlier index (of the string) to a later index. So, in the worst-case, every index may have edges to every other index that come afterwards.

Say $P(i)$ is the count of distinct paths that has $i$ as its starting point. Then $P(0)$ would give the worst-case path count. Since, $i$ -th index can use any of the later indices as its successor:

$P(i) = \begin{cases} 1, & \text{if } i = n-1 \\ \sum_{j = i+1}^{n-1} P(j) & \text{otherwise} \end{cases}$

Note, $P(i) = P(i+1) + \sum_{j=i+2}^{n-1} P(j)$ and $P(i+1) = \sum_{j=i+2}^{n-1} P(j)$ . Therefore, $P(i) = 2 \cdot P(i+1)$ . So, $P(0) = \mathcal{O}(2^n)$ . A path, in the worst-case, can have $n$ indices. For each distinct path, we also do a $\mathcal{O}(n)$ construct_sentence(). As a result, total time complexity is $\mathcal{O}(n \cdot 2^n) + \mathcal{O}(n \cdot 2^n) = \mathcal{O}(n \cdot 2^n)$ .

Disregarding output size, extra space complexity is the worst-case size of the adj_list, so: $\mathcal{O}(n^2)$ .

class Solution:
    def construct_sentence(self, s: str, path: List[int]) -> str:
        words = []
        for i in range(len(path)-1):
            begin, end = path[i], path[i+1]
            words.append( s[begin:end] )
        return " ".join(words)
 
    def dfs(self, s: str, adj_list: Dict[int, List[int]], u: int, path: deque[int], sentences: List[str]) -> None:
        if u == len(s):
            sentences.append( self.construct_sentence(s, list(path)+[u]) )
            return
 
        path.append(u)
        for v in adj_list[u]:
            self.dfs(s, adj_list, v, path, sentences)
        path.pop()
 
    def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:
        word_set = set(wordDict)
        n = len(s)
        adj_list = defaultdict(list)
        dp = [True] + [False]*n
        for i in range(1, n+1):
            for j in range(i, 0, -1):
                if not dp[j-1]:
                    continue
                if s[j-1:i] not in word_set:
                    continue
                dp[i] = True
                adj_list[j-1].append(i)
        if not dp[n]:
            return []
         
        sentences = []
        self.dfs(s, adj_list, 0, deque(), sentences)
        return sentences

W(n) as root

class Solution:
    def construct_sentence(self, s: str, path: List[int]) -> str:
        words = []
        for i in range(len(path)-1):
            begin, end = path[i], path[i+1]
            words.append( s[begin:end] )
        return " ".join(words)
 
    def dfs(self, s: str, adj_list: Dict[int, List[int]], u: int, path: deque[int], sentences: List[str]) -> None:
        if u == 0:
            sentences.append( self.construct_sentence(s, [u]+list(path)) )
            return
 
        path.appendleft(u)
        for v in adj_list[u]:
            self.dfs(s, adj_list, v, path, sentences)
        path.popleft()
 
    def wordBreak(self, s: str, wordDict: List[str]) -> List[str]:
        word_set = set(wordDict)
        n = len(s)
        adj_list = defaultdict(list)
        dp = [True] + [False]*n
        for i in range(1, n+1):
            for j in range(i, 0, -1):
                if not dp[j-1]:
                    continue
                if s[j-1:i] not in word_set:
                    continue
                dp[i] = True
                adj_list[i].append(j-1)
        if not dp[n]:
            return []
         
        sentences = []
        self.dfs(s, adj_list, n, deque(), sentences)
        return sentences

unreasonably effective