LeetCode 91: Decode Ways

Decodings can be thought of as paths in a binary tree. So, we need to count the number of paths.

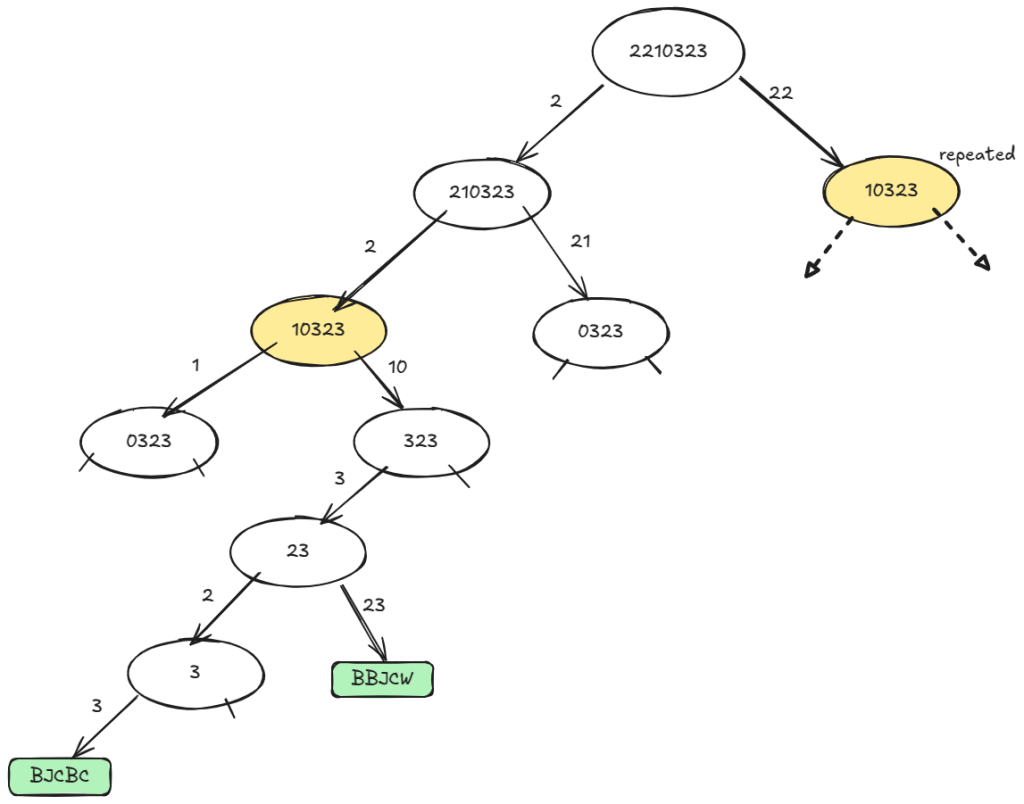
Note, we do not need to keep track of already counted decodings. In the example above, the first decision at the root produced two branches: (1) starts with “2” having symbol “B” (2) starts with “22” having symbol “V”. So, at least this first symbol will be different between a path on the left half and a path on the right half. This reasoning applies recursively to subtrees in either half as well.

Dynamic programming

Subproblem

Let $D(i)$ be the number of ways the suffix $x_i, \ldots ,x_{n-1}, x_n$ can be decoded. Then:

$D(i) = \begin{cases} 1, & \text{if } i = n+1 \\ 0, & \text{if } x_i = ``0" \\ 1, & \text{if } i = n \\ D(i+1), & \text{if } \texttt{num}\left( x_i, x_{i+1} \right) > 26 \\ D(i+1) + D(i+2) & \text{otherwise} \end{cases}$

$D(n+1)$ represents empty suffix, meaning the input str has been decoded successfully, so $D(n+1) = 1$ .

Order

Since edges flow from later to earlier indices, we process the input str right-to-left.

Top-down with memoization

There are only $\mathcal{O}(n)$ distinct subproblems and with memoization we should be solving a subproblem only once. So, time: $\mathcal{O}(n)$ , space: $\mathcal{O}(n)$ .

If we did not use memoization, in the worst-case, the recursion tree could have depth $\mathcal{O}(n)$ and width would have doubled level-to-level. Total time would have been $\mathcal{O}(2^n)$ . So, there must be a lot of overlapping subproblems.

class Solution:
    def dfs(self, s: str, begin: int, memo: Dict[int, int]) -> int:
        if begin in memo:
            return memo[begin]
        if begin == len(s):
            return 1
        if s[begin] == '0':
            memo[begin] = 0
            return memo[begin]
        if begin == len(s)-1:
            return 1
        
        # Consume one digit
        count = self.dfs(s, begin+1, memo)
        if int( s[begin:begin+2] ) > 26:
            memo[begin] = count
            return memo[begin]
        # Consume two digits
        count += self.dfs(s, begin+2, memo)
        memo[begin] = count
        return memo[begin]

    def numDecodings(self, s: str) -> int:
        return self.dfs(s, 0, dict())

Bottom-up

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(n)$ .

class Solution:
    def numDecodings(self, s: str) -> int:
        n = len(s)
        dp = [0] * (n+1)
        dp[n] = 1
        dp[n-1] = 0 if s[n-1] == '0' else 1
        for i in range(n-2, -1, -1):
            if s[i] == '0':
                continue
            dp[i] = dp[i+1]
            if int( s[i:i+2] ) <= 26:
                dp[i] += dp[i+2]
        return dp[0]

A subproblem depends on just two immediately succeeding subproblems, so we can use two variables instead of $n$ -sized dp.

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(1)$ .

class Solution:
    def numDecodings(self, s: str) -> int:
        n = len(s)
        dp = [0] * 2
        second = 0 if s[n-1] == '0' else 1
        first = 1
        for i in range(n-2, -1, -1):
            first, second = second, first
            if s[i] == '0':
                second = 0
                continue
            second = first if int( s[i:i+2] ) > 26 else first+second
        return second

unreasonably effective