unreasonably effective

you can be sloppy, as long as you are rigorous

LeetCode 268: Missing Number

link

Math

Difference between expected sum \sum_{x=0}^{n} x = \frac{n (n+1)}{2} and actual sum is the missing number.

Time: \mathcal{O}(n), space: \mathcal{O}(1).

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        n = len(nums)
        expected_sum = (n * (n+1)) // 2
        return expected_sum - sum(nums)

Cyclic sort

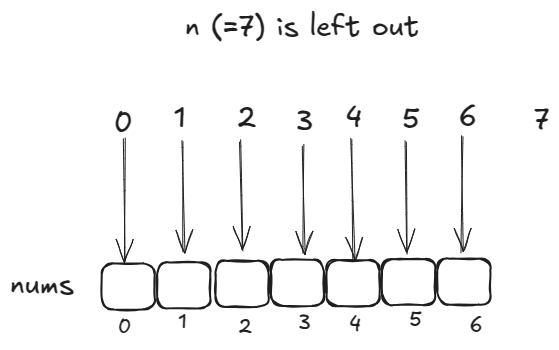
If we think about how nums would look like once sorted, there are two options:

  • n is left out. Then, i = nums[i] for i \in \{0, 1, 2, \ldots, n-1\}.
  • n has been swapped in place of j. Then, i = nums[i] for i \in \{0, 1, \ldots, n-1\} \setminus \{ j \} and nums[j] = n.

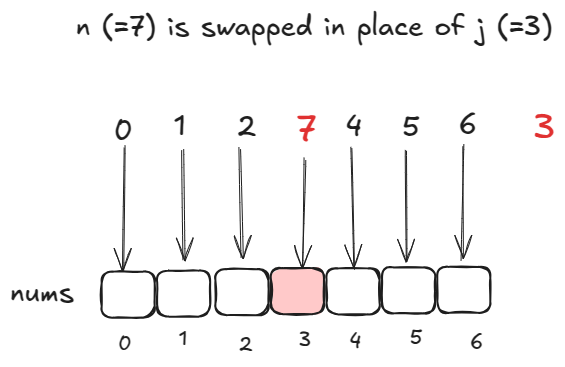
So, if we put each nums[i] in its expected index, there will be zero (first option) or one (second option) index not matching its value.

Time: \mathcal{O}(n), space: \mathcal{O}(1).

class Solution:
    def cyclic_sort(self, nums: List[int], begin: int, end: int, offset: int) -> None:
        for i in range(begin, end):
            while (
                nums[i] != i - begin + offset
                and (j := begin + nums[i] - offset) < end
                and nums[i] != nums[j]
            ):
                nums[i], nums[j] = nums[j], nums[i]

    def find_first_mismatch(self, nums: List[int], begin: int, end: int, offset: int) -> Tuple[int, int]:
        for i in range(begin, end):
            if ( expected := i-begin+offset ) != nums[i]:
                return expected, nums[i]
        return end-begin+offset, None

    def missingNumber(self, nums: List[int]) -> int:
        begin, end, offset = 0, len(nums), 0
        self.cyclic_sort(nums, 0, len(nums), 0)
        missing, _ = self.find_first_mismatch(nums, begin, end, offset)
        return missing

tanvirdotzaman

Leave a comment