We want to build a directed graph where vertex set is the alien alphabet and an edge 
Single word
Say words = ["confide"]. With a single word we do not know anything about the ordering between the letters. We can emit the unique letters in the word in any order. As a consequence, we can always add distinct letters from the alien words to the graph as vertices, even if no edges flow to or from them.
Two words
Say words = ["confide", "conflate"]. From the first mismatch ("i" vs. "l"), we would know the edge: 
So, the two words may have three regions: (1) common prefix (2) mismatch (3) suffix. If (2) is present we can infer one edge of the graph. Otherwise, the order is valid except when next word is a proper prefix. Because, if a word is a proper prefix of another, in lexicographic order, the shorter one must come first.
Since it is always a mismatch that contributes an edge, the graph will not have self loop.
Three words
Comparison between (1st and 2nd) or between (2nd and 3rd) words is like comparing two-word input. However, no new information is gained from comparing (1st and 3rd) words. Later (fourth and onwards) words — if compared against 1st — do not give new information either. As a result, we shall compare pairs of consecutive words while building the graph.
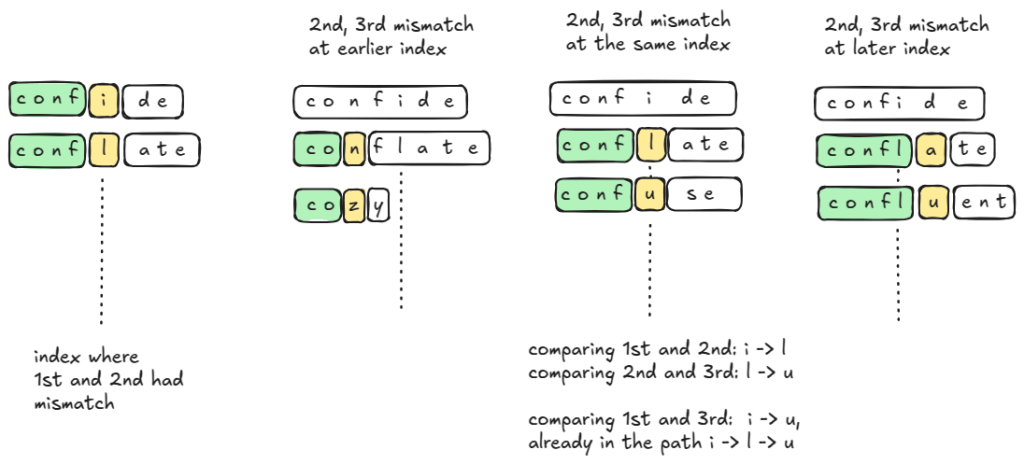
We note that 
class Solution:
# O(m): m is length of longest word
def find_edge(self, curr_word, next_word) -> Tuple[str, str]:
n = min(len(curr_word), len(next_word))
i = 0
while i < n:
if (u := curr_word[i]) != (v := next_word[i]):
return u, v
i += 1
if len(curr_word) <= len(next_word):
return ("", "")
return None
def add_vertices(self, word, adj_list) -> None:
for c in word:
if c not in adj_list:
adj_list[c] = set()
# O(n * m): n words, m is longest word len
def build_graph(self, words) -> Dict[str, Set[str]]:
adj_list = {}
for i, curr_word in enumerate(words):
self.add_vertices( curr_word, adj_list )
# no next word
if i == len(words)-1:
break
next_word = words[i+1]
edge = self.find_edge( curr_word, next_word )
# invalid: next_word is a proper prefix of curr_word
if not edge:
return None
u, v = edge
if u and v:
adj_list[u].add(v)
return adj_list
def is_back_edge(self, u, v, visited, onstack) -> bool:
return (v in visited) and (v in onstack)
def explore_cycle(self, u, adj_list, visited, onstack) -> bool:
visited.add(u)
onstack.add(u)
for v in adj_list[u]:
if self.is_back_edge(u, v, visited, onstack):
return True
if v in visited:
continue
if self.explore_cycle(v, adj_list, visited, onstack):
return True
onstack.remove(u)
return False
def has_cycle(self, adj_list) -> bool:
visited, onstack = set(), set()
for u in adj_list:
if u in visited:
continue
if self.explore_cycle(u, adj_list, visited, onstack):
return True
return False
def explore_post(self, u, adj_list, visited, post_inc):
visited.add(u)
for v in adj_list[u]:
if v in visited:
continue
self.explore_post(v, adj_list, visited, post_inc)
post_inc.append(u)
def sorted_topo(self, adj_list) -> List[str]:
visited = set()
post_inc = []
for u in adj_list:
if u in visited:
continue
self.explore_post(u, adj_list, visited, post_inc)
return post_inc[::-1]
def alienOrder(self, words: List[str]) -> str:
# O(n * m)
adj_list = self.build_graph(words)
if not adj_list:
return ""
# O(1)
contradict = self.has_cycle(adj_list)
if contradict:
return ""
# O(1)
lex_sorted = self.sorted_topo(adj_list)
return "".join( lex_sorted )
Instead of using separate DFS’s to find cycle and topological order, we can do both in a single DFS.
class Solution:
# O(m): m is length of longest word
def find_edge(self, curr_word, next_word) -> Tuple[str, str]:
n = min(len(curr_word), len(next_word))
i = 0
while i < n:
if (u := curr_word[i]) != (v := next_word[i]):
return u, v
i += 1
if len(curr_word) <= len(next_word):
return ("", "")
return None
def add_vertices(self, word, adj_list) -> None:
for c in word:
if c not in adj_list:
adj_list[c] = set()
# O(n * m): n words, m is longest word len
def build_graph(self, words) -> Dict[str, Set[str]]:
adj_list = {}
for i, curr_word in enumerate(words):
self.add_vertices( curr_word, adj_list )
# no next word
if i == len(words)-1:
break
next_word = words[i+1]
edge = self.find_edge( curr_word, next_word )
# invalid: next_word is a proper prefix of curr_word
if not edge:
return None
u, v = edge
if u and v:
adj_list[u].add(v)
return adj_list
def is_back_edge(self, u, v, visited, onstack) -> bool:
return (v in visited) and (v in onstack)
def explore(self, u, adj_list, visited, onstack, post_order) -> bool:
visited.add(u)
onstack.add(u)
cycle_found = False
for v in adj_list[u]:
if self.is_back_edge(u, v, visited, onstack):
cycle_found = True
if v in visited:
continue
cycle_found = cycle_found or self.explore(v, adj_list, visited, onstack, post_order)
onstack.remove(u)
post_order.append(u)
return cycle_found
def inspect_graph(self, adj_list) -> Tuple[bool, List[int]]:
visited, onstack = set(), set()
has_cycle, post_order = False, []
for u in adj_list:
if u in visited:
continue
has_cycle = has_cycle or self.explore(u, adj_list, visited, onstack, post_order)
return has_cycle, post_order[::-1]
def alienOrder(self, words: List[str]) -> str:
adj_list = self.build_graph(words)
if not adj_list:
return ""
has_cycle, lex_sorted = self.inspect_graph(adj_list)
if has_cycle:
return ""
return "".join( lex_sorted )
unreasonably effective 
Leave a comment