LeetCode 2246: Longest Path With Different Adjacent Characters

link

If we had a simpler tree where for edge $(u, v)$ , s[u] != s[v], then our problem would be finding the length of the longest path in the tree.

We can reduce the original problem to the above simpler problem by building an undirected graph having an edge only between different char’s. This is equivalent to deleting edges from the original tree having same char as endpoints.

DFS per leaf

In a tree, the longest path starts at some leaf — a node having 0 or 1 edge.

Because, say $\langle u \ldots v \rangle$ is the longest path and $u$ is not a leaf. So, $u$ has at least two edges. Say these two edges are: $(u, x)$ and $(u, y)$ . Say $(u, y)$ is included in the path $\langle u \ldots v \rangle$ . We can now have a longer path: $\langle x, u \ldots v \rangle$ — producing a contradiction.

As a result, in our new graph, we can do DFS starting from each leaf and take the length of the longest path across the leaves.

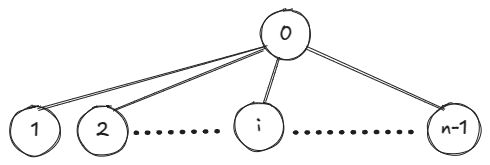
A very wide tree like below will have many leaves and each DFS from a leaf will explore all $n$ edges.

Time: $\mathcal{O}(n^2)$ , space: $\mathcal{O}(n)$ .

class Solution:
    def build_graph(self, parent: List[int], s: str) -> Dict[int, Set[int]]:
        adj_list = { u : set() for u in range( len(parent) ) }
        for u, v in enumerate(parent[1:], start=1):
            if s[u] == s[v]:
                continue
            adj_list[u].add(v)
            adj_list[v].add(u)
        return adj_list

    def max_len_after(self, u, adj_list, visited) -> int:
        visited.add(u)

        max_len = 0
        for v in adj_list[u]:
            if v in visited:
                continue
            max_len = max( max_len, 1 + self.max_len_after(v, adj_list, visited) )
        return max_len

    def longestPath(self, parent: List[int], s: str) -> int:
        adj_list = self.build_graph(parent, s)

        leaves = [u for u, edges in adj_list.items() if len(edges) <= 1]

        max_len = 0
        for u in leaves:
            max_len = max( max_len, 1 + self.max_len_after(u, adj_list, set()) )
        
        return max_len

DFS per connected component

Note, the original tree is a single connected component. Since a tree is connected and there are minimal, only $(n-1)$ edges between $n$ nodes, deleting every edge increases count of connected components by 1. So, our new graph is a forest of trees. No edges flow between the connected components. As long as we can find the longest path length for one tree with a single DFS, we can run DFS per connected component and take the max length across them. Total time will be linear in the size of the forest.

In a tree, longest path can be of two types: (1) chain (2) arc. We can take max between these two types. Note, an arc-type path including $u$ as its root, cannot contribute to a longest path that includes $u$ ‘s parent.

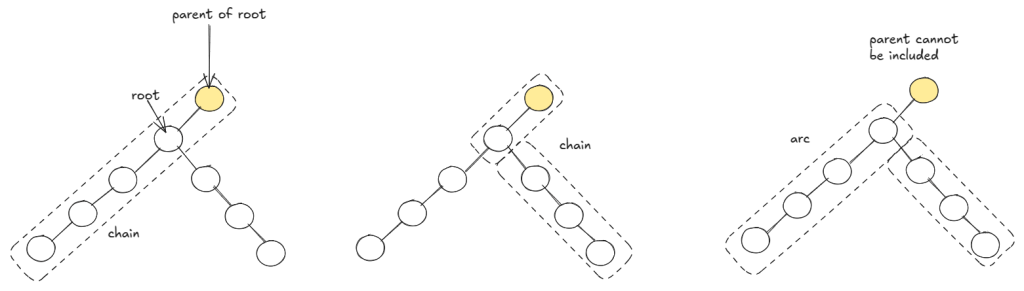
For a single connected component, we can run DFS once to find both types of maxes in the following way.

Say, $C(u)$ represents chain-type longest path length of a tree that is rooted at $u$ . Then, $C(u) = 1 + \max{ \left( \{ C(v) : (u, v) \in E \} \right) }$ .

Say $A(u)$ represents arc-type longest path length of a tree that is rooted at $u$ and $A_{\texttt{node}}(u)$ represents arc-type longest path length including $u$ . Note, $A(u)$ may not include $u$ . Then,

$A(u) = \max{ \left( \{A_{\texttt{node}}(u)\} \cup \{ A(v) : (u, v) \in E \} \right) }$ and $A_{\texttt{node}}(u) = 1 + \max{ \left( \{ C(v) : (u, v) \in E \} \right) } + \texttt{second-max}\left( \{C(v) : (u, v) \in E \} \right)$ .

Max length for a connected component (cc) is then $\max{ \left( \{ C(\texttt{cc\_root}), A(\texttt{cc\_root}) \} \right) }$ .

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(n)$ .

class Solution:
    def build_graph(self, parent: List[int], s: str) -> Dict[int, Set[int]]:
        adj_list = { u : set() for u in range( len(parent) ) }
        for u, v in enumerate(parent[1:], start=1):
            if s[u] == s[v]:
                continue
            adj_list[u].add(v)
            adj_list[v].add(u)
        return adj_list

    def tree_max(self, root, adj_list, visited) -> Tuple[int, int]:
        visited.add(root)

        child_chain_max, child_chain_second_max = 0, 0
        child_arc_max = 0
        for v in adj_list[root]:
            if v in visited:
                continue
            child_chain, child_arc = self.tree_max(v, adj_list, visited)
            
            child_arc_max = max(child_arc_max, child_arc)
            
            if child_chain < child_chain_second_max:
                continue
            if child_chain > child_chain_max:
                child_chain_max, child_chain_second_max = child_chain, child_chain_max
            else:
                child_chain_second_max = child_chain
        
        root_chain_max = 1 + child_chain_max
        root_arc_max = 1 + child_chain_max + child_chain_second_max
        root_global_arc_max = max(child_arc_max, root_arc_max)
        return root_chain_max, root_global_arc_max

    def longestPath(self, parent: List[int], s: str) -> int:
        adj_list = self.build_graph(parent, s)

        visited = set()
        max_len = 0
        for u in adj_list:
            if u in visited:
                continue
            # Another connected component
            cc_chain_max, cc_arc_max = self.tree_max(u, adj_list, visited)
            max_len = max(max_len, cc_chain_max, cc_arc_max)
        
        return max_len

Since it is a tree and we are going downwards from root, we can use a directed graph with parent-to-child edges only. The adjacency list takes up half the space. We also do not need to skip visited nodes within a DFS. However, to skip exploring a connected component more than once, we still keep visited in the outer loop.

class Solution:
    def build_graph(self, parent: List[int], s: str) -> Dict[int, Set[int]]:
        adj_list = { u : set() for u in range( len(parent) ) }
        for c, p in enumerate(parent[1:], start=1):
            if s[c] == s[p]:
                continue
            adj_list[p].add(c)
        return adj_list

    def tree_max(self, root, adj_list, visited) -> Tuple[int, int]:
        visited.add(root)

        child_chain_max, child_chain_second_max = 0, 0
        child_arc_max = 0
        for v in adj_list[root]:
            child_chain, child_arc = self.tree_max(v, adj_list, visited)
            
            child_arc_max = max(child_arc_max, child_arc)
            
            if child_chain < child_chain_second_max:
                continue
            if child_chain > child_chain_max:
                child_chain_max, child_chain_second_max = child_chain, child_chain_max
            else:
                child_chain_second_max = child_chain
        
        root_chain_max = 1 + child_chain_max
        root_arc_max = 1 + child_chain_max + child_chain_second_max
        root_global_arc_max = max(child_arc_max, root_arc_max)
        return root_chain_max, root_global_arc_max

    def longestPath(self, parent: List[int], s: str) -> int:
        adj_list = self.build_graph(parent, s)

        visited = set()
        max_len = 0
        for u in adj_list:
            if u in visited:
                continue
            # Another connected component
            cc_chain_max, cc_arc_max = self.tree_max(u, adj_list, visited)
            max_len = max(max_len, cc_chain_max, cc_arc_max)
        
        return max_len

unreasonably effective