unreasonably effective

you can be sloppy, as long as you are rigorous

LeetCode 2115: Find All Possible Recipes from Given Supplies

link

We build a directed graph with vertex set as the union of recipes and ingredients. An edge (u \rightarrow v) represents u\ \texttt{is-required-to-make}\ v. A topological order of recipes from this graph will give us the recipes we can make.

We use in-degree approach. Say we start with supplies as the sources, therefore vertices with in-degree = 0. Then the new sources found at the end of 1st iteration are the recipes we were able to make using the supplies and they have become our new supplies. We keep peeling layers of sources and accumulate can-be-made recipes which is also a topological order of a subset of recipes. If a recipe never becomes a source, it cannot be made.

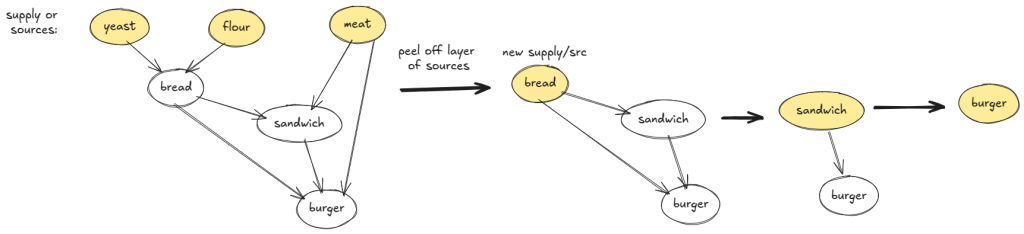
Time and space is linear in the size of the graph. Say \mathcal{R} is the set of recipes, \mathcal{I} is the set of ingredients, and m is the max number of ingredients needed for a recipe. Then, the size of vertex set is | \mathcal{R} \cup \mathcal{I} | and the size of edge set is \mathcal{O}(m \cdot |\mathcal{R}|).

So, time and space complexity: \mathcal{O}\left( | \mathcal{R} \cup \mathcal{I} | + m \cdot |\mathcal{R}| \right)

class Solution:
    def build_graph(self, recipes, ingredients) -> Dict[str, Set[str]]:
        # V: { recipes U ingredients }
        # E: { (u, v) : u is-required-for v }
        adj_list = defaultdict(set)
        for i, r in enumerate(recipes):
            for ing in ingredients[i]:
                adj_list[ing].add(r)
        return adj_list

    def build_indegree_map(self, adj_list) -> Dict[str, int]:
        inmap = defaultdict(int)
        for u in adj_list:
            for v in adj_list[u]:
                inmap[v] += 1
        return inmap

    def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:
        adj_list = self.build_graph( recipes, ingredients )
        inmap = self.build_indegree_map( adj_list )

        curr_sources = supplies
        topo_order = []
        while curr_sources:
            new_sources = []
            for u in curr_sources:
                for v in adj_list[u]:
                    inmap[v] -= 1
                    if inmap[v] == 0:
                        new_sources.append(v)
            topo_order.extend(new_sources)
            curr_sources = new_sources
        return topo_order

tanvirdotzaman

,

Leave a comment