LeetCode 1300: Sum of Mutated Array Closest to Target

Brute Force

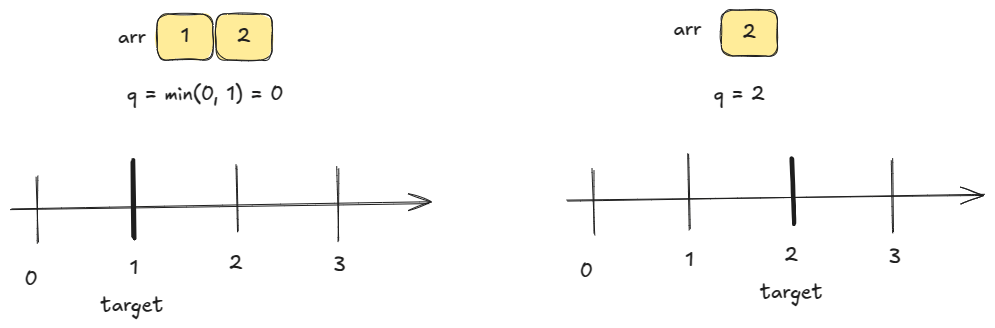
We need to find the best $q$ defined as: $\texttt{arg-min}_{q \in \mathbb{Z}} \bigl\lvert \sum_i \min{(q, x_i)} - \texttt{target} \bigr\rvert$ . We break a tie in favor of smaller $q$ .

Since all numbers in arr are positive integers, the domain of $q$ is $\{ 0, 1, 2, \ldots, \texttt{target} \}$ .

Time: $\mathcal{O}(\texttt{target} \cdot n)$ , space: $\mathcal{O}(1)$ .

class Solution:
    def findBestValue(self, arr: List[int], target: int) -> int:
        min_diff, best_q = float('inf'), float('inf')
        for q in range(target+1):
            capped_sum = sum( min(q, x) for x in arr )

            diff = abs( target - capped_sum )
            if diff > min_diff:
                continue
            
            best_q = min(best_q, q) if diff == min_diff else q
            min_diff = diff
        
        return best_q

Sort and search

We can break the inner sum to get rid of $\min( \cdot )$ like: $\sum_{x_i < q} x_i + \sum_{x_i \ge q} q$ . In the input arr, these two cases are mixed. We can sort arr to separate them out. Then with binary-search, we can find these two regions and with a pre-computed cumsum, the inner loop takes $\mathcal{O}(\lg{n})$ .

Time: $\mathcal{O}( \texttt{target} \cdot \lg{n} )$ , space: $\mathcal{O}(n)$ .

class Solution:
    def find_insert_index(self, x, nums) -> int:
        lo, hi = 0, len(nums)-1
        while lo <= hi:
            mid = (lo + hi) // 2
            if nums[mid] < x:
                lo = mid+1
            else:
                hi = mid-1
        return lo

    def find_capped_sum(self, q, arr, cumsum) -> int:
        n = len(arr)
        q_pos = self.find_insert_index(q, arr)
        left_sum = cumsum[q_pos-1] if q_pos > 0 else 0
        right_sum = (n - q_pos)*q

        return left_sum + right_sum

    def find_cumsum(self, nums) -> List[int]:
        cumsum = [nums[0]] + [0] * (len(nums)-1)
        for i, x in enumerate(nums[1:], start=1):
            cumsum[i] = cumsum[i-1] + x
        return cumsum

    def findBestValue(self, arr: List[int], target: int) -> int:
        arr.sort()
        cumsum = self.find_cumsum(arr)
        min_diff, best_q = float('inf'), float('inf')
        for q in range(target+1):
            capped_sum = self.find_capped_sum(q, arr, cumsum)

            diff = abs( target - capped_sum )
            if diff > min_diff:
                continue
            
            best_q = min(best_q, q) if diff == min_diff else q
            min_diff = diff
        
        return best_q

Given a target and arr of length $n$ , we have perfect size $p = \frac{ \texttt{target} }{ n }$ — if we take $n$ copies of this size we meet target perfectly. Since we are allowed to cap, as long as arr has all numbers at least as big as $p$ , we are allowed to use $p$ as our answer.

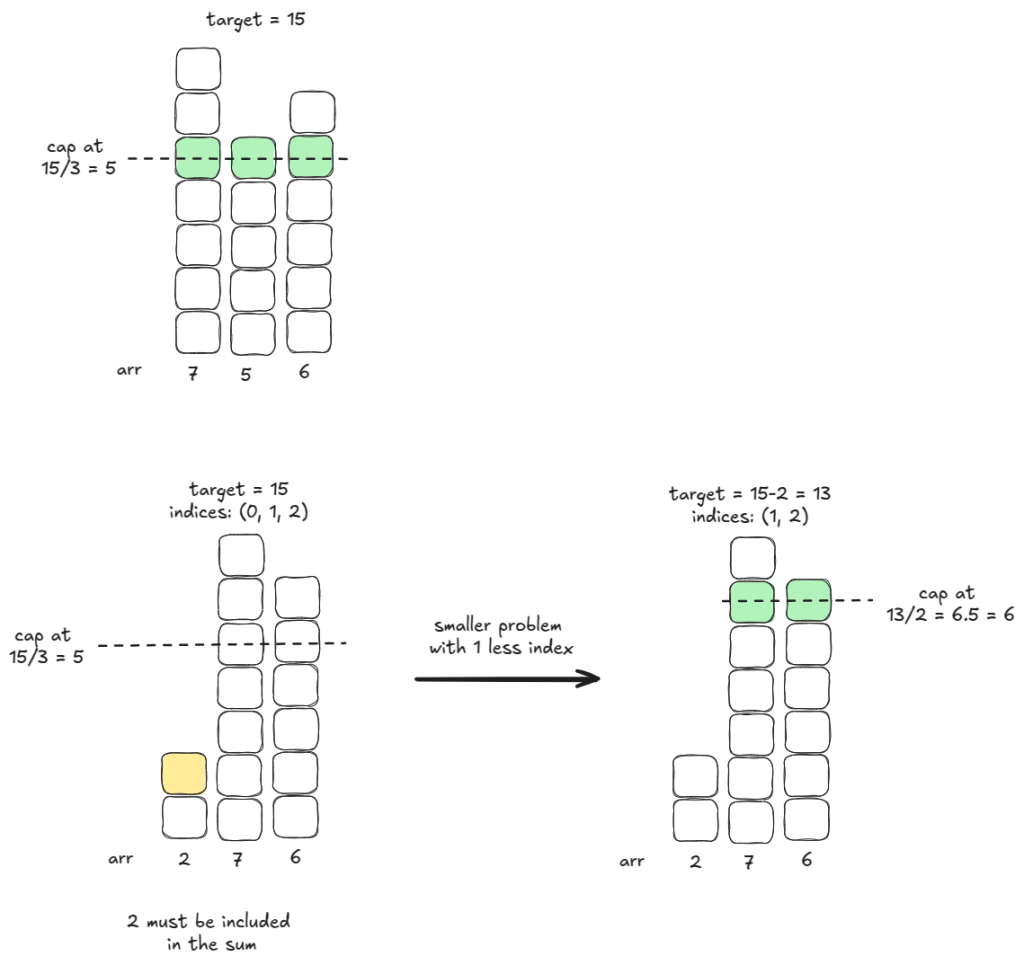
If a number in arr is smaller than $p$ , we have to include that number and find a perfect size for the remainder of the arr. If arr was sorted, as soon as we find an allowed perfect size for the suffix arr[j:n+1], we can return the closest number to the perfect size $\frac{ \texttt{target} - \sum_{i=0}^{j} \texttt{arr}[i] }{ n-j }$ as the answer.

Time: $\mathcal{O}(n \cdot \lg{n})$ . Space: $\mathcal{O}(n)$ .

class Solution:
    def find_best(self, begin, arr, target) -> int:
        if begin == len(arr):
            return arr[-1]
        
        x = arr[begin]
        n = len(arr) - begin
        if n*x < target:
            return self.find_best(begin+1, arr, target-x)
        
        x_fit = ceil( target/n - 0.5 )
        return x_fit

 
    def findBestValue(self, arr: List[int], target: int) -> int:
        arr.sort()
        return self.find_best(0, arr, target)

We can do it iteratively to save space.

Time: $\mathcal{O}(n \cdot \lg{n})$ . Space: that of sorting.

class Solution:
    def findBestValue(self, arr: List[int], target: int) -> int:
        arr.sort()
        n = len(arr)
        for i, x in enumerate(arr):
            ncopies = n-i
            if ncopies * x < target:
                # If x is too small, must include
                target -= x
                continue
            return ceil(target/ncopies - 0.5)
        return arr[-1]

unreasonably effective