LeetCode 354: Russian Doll Envelopes

Longest Increasing Subsequence: Dynamic Programming

We need to find the largest subset of envelopes which can be ordered as an increasing sequence. Sorting by width, makes it the problem of finding the length of longest increasing subsequence.

Time: $\mathcal{O}(n^2)$ , space: $\mathcal{O}(n)$ .

class Solution:
    def maxEnvelopes(self, envelopes: List[List[int]]) -> int:
        def is_bigger(x, y):
            return x[0] > y[0] and x[1] > y[1]
 
        envelopes.sort()
        n = len(envelopes)
        dp = [1] + [0] * (n-1)
        for i in range(1, n):
            sub_max = 0
            for j in range(i-1, -1, -1):
                if not is_bigger(envelopes[i], envelopes[j]):
                    continue
                sub_max = max( sub_max, dp[j] )
            dp[i] = 1 + sub_max
 
        return max(dp)

Longest Increasing Subsequence: Binary Search

Once we sort the envelopes by width, the problem becomes finding the length of the longest increasing sub-sequence of the heights (taking care of duplicate widths).

We make below two observations about an increasing sequence:

If correctly maintaining the length of an increasing sequence is our only concern (do not care about the actual sequence), we can just keep two pieces of information about it: the largest number and its current length. So, while considering the next number, as long as we take care of updating these two pieces of information we should be good with the length.
If finding longer increasing sequences is our goal, then for an existing increasing sequence $\langle x_1, x_2, x_3, \ldots, x_i, x_j \rangle$ , a number $y$ is a better choice as the largest if $x_i < y < x_j$ . It keeps the length correct but improves potential for the increasing sequence to grow in the future.

With these we can efficiently find the length of the longest increasing sequence following two steps:

Extend: Append $y$ to current increasing sequence $\langle x_1, x_2, x_3, \ldots, x_i, x_j, \ldots, x_n \rangle$ only if $x_n < y$ , increasing the length by 1.
Replace: If $y \le x_n$ we replace $x_j$ with $y$ given $x_i < y \le x_j$ . To find the replacement index $j$ we use binary-search.

For our problem, we want both height and width to be increasing. If there are multiple envelopes having the same width but different heights, finding the length of the longest increasing sub-sequence considering only heights might overshoot — we may include some heights which are prohibited by width. An example below:

To prevent that, we primary-sort by width as before, but secondary-sort by negative of height. As a result, the duplicate widths are now sorted in non-increasing order of height.

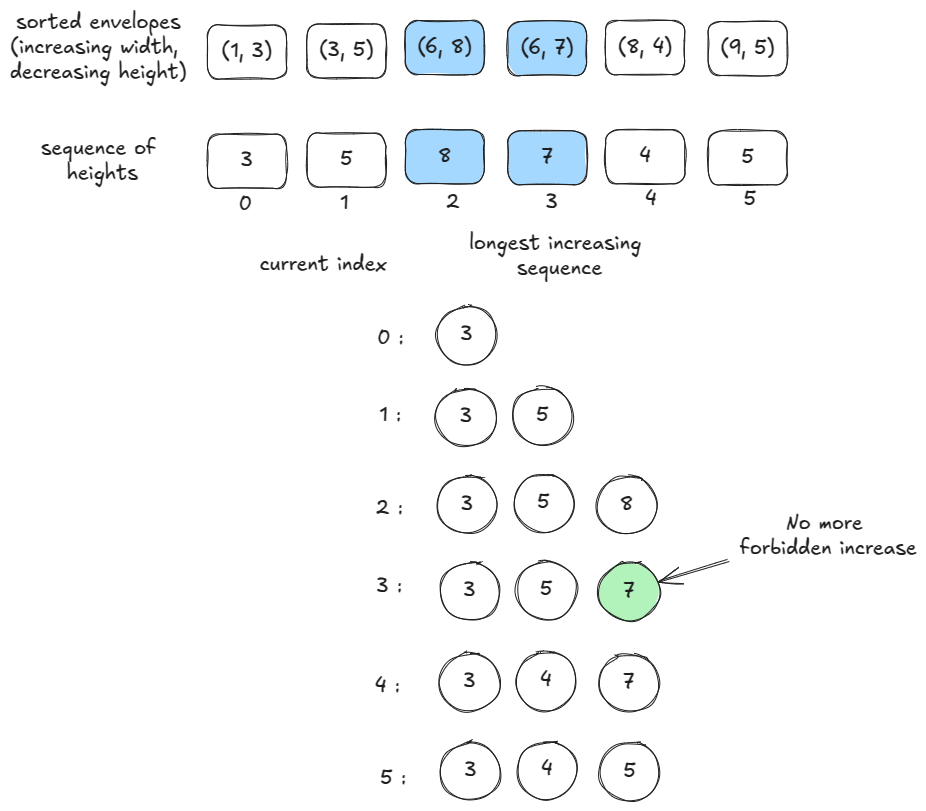
Time: $\mathcal{O}(n \cdot \lg{n})$ , space: that of sorting.

class Solution:
    def find_better_replacement(self, x, nums) -> int:
        lo, hi = 0, len(nums)-1
        while lo <= hi:
            mid = (lo+hi) // 2
            if nums[mid] < x:
                lo = mid+1
            else:
                hi = mid-1
        # [      <      |       >=     ]
        # --------------|lo-------------
        # 
        # Replacement y is better when: nums[lo-1] < y < nums[lo]
        # Possible, nums[lo] == y, that would not hurt
        return lo
 
    def maxEnvelopes(self, envelopes: List[List[int]]) -> int:
        # Sort by increasing width, decreasing height
        envelopes.sort(key=lambda dims: (dims[0], -dims[1]))
         
        # Now find len of longest increasing subsequence of heights
        increasing_heights = []
        for _, height in envelopes:
            replace_pos = self.find_better_replacement( height, increasing_heights )
            # height is larger than largest, take it in
            if replace_pos == len(increasing_heights):
                increasing_heights.append( height )
                continue
             
            # Potentially better choice
            increasing_heights[replace_pos] = height
 
        return len( increasing_heights )

unreasonably effective