Rotation of the matrix is composed of smaller, independent rotations each of which takes constant extra space.
The matrix can be thought of as a collection of concentric disks. Within each disk there are 4-element loops. We can rotate each loop with just one extra variable.
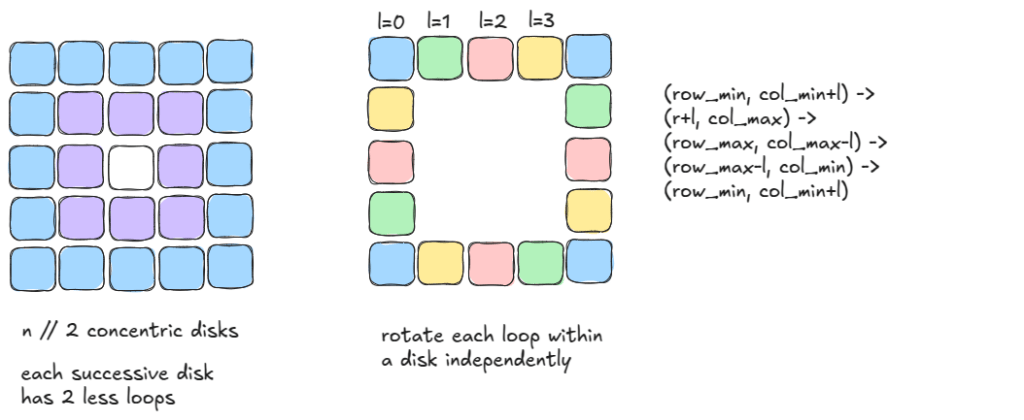
The four transitions within a loop involve: row_min, row_max, col_min, col_max, and loop index. We can deduce all of these from the disk index and 
Time: 
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
disk_count = n // 2
for d in range(disk_count):
row_min, col_min = d, d
row_max, col_max = n-1-d, n-1-d
loop_count = n-1-2*d
for l in range(loop_count):
tmp = matrix[row_min+l][col_max]
matrix[row_min+l][col_max] = matrix[row_min][col_min+l]
tmp, matrix[row_max][col_max-l] = matrix[row_max][col_max-l], tmp
tmp, matrix[row_max-l][col_min] = matrix[row_max-l][col_min], tmp
matrix[row_min][col_min+l] = tmp
unreasonably effective 
Leave a comment