Per row binary search
Since rows are sorted, for each row we find the would-be insert index of using binary-search which gives the negative count for that row.
Time: , space:
.
class Solution:
def find_insert_index(self, x, nums) -> int:
# [ >= | < ]
# ----------|lo------
lo, hi = 0, len(nums)-1
while lo <= hi:
mid = (lo+hi) // 2
if nums[mid] < x:
hi = mid-1
else:
lo = mid+1
return lo
def count_negatives_in_row(self, row) -> int:
first_negative_index = self.find_insert_index(0, row)
return len(row) - first_negative_index
def countNegatives(self, grid: List[List[int]]) -> int:
count = 0
for row in grid:
count += self.count_negatives_in_row(row)
return count
Trace negative boundary
Since the grid is sorted both row-wise and column-wise, at each coordinate we have two directions with “opposite” gradients: one decreasing and one increasing. Using this, starting either from (0, n-1) or (m-1, 0), we can trace the negative boundary and count. If current cell is >= 0, we can follow the decreasing direction. If the cell is < 0, we can follow the increasing direction.
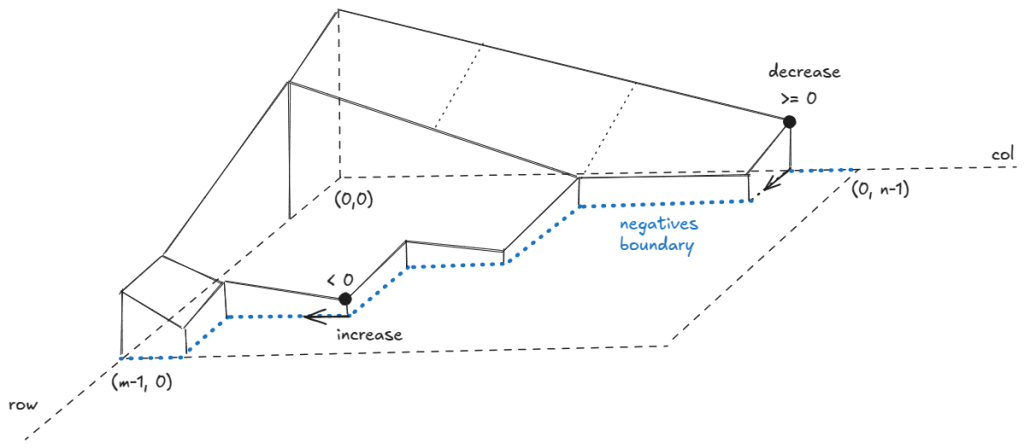
Time: , space:
.
class Solution:
def countNegatives(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
r, c = 0, n-1
count = 0
while r < m and c >= 0:
if grid[r][c] >= 0:
r += 1
continue
count += (m-r)
c -= 1
return count
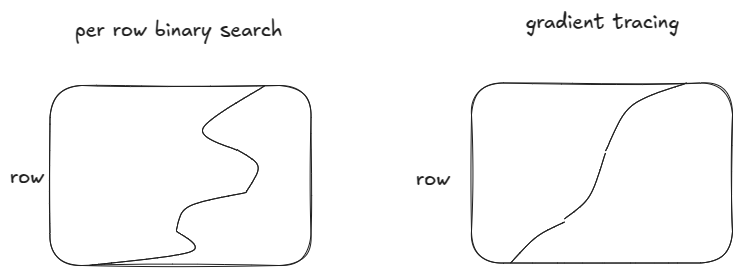
Per row binary search is more generic. Gradient based tracing works when the boundary is monotonic.
Leave a comment