unreasonably effective

link

The bounding box’s width is determined by the leftmost and the rightmost occurrences of “1” across all rows. Similarly, the height is determined by the topmost and the bottom-most rows where ones appear.

Linear search per row

In each row we can linearly search for the leftmost and the rightmost columns having ones.

Time: , space: .

class Solution:
    def find_row_ones(self, row) -> Tuple[int]:
        left_col, right_col = float('inf'), float('-inf')
        for c, x in enumerate(row):
            if x == '0':
                continue
            left_col, right_col = min(left_col, c), max(right_col, c)
        
        return (left_col, right_col) if left_col != float('inf') else ()

    def minArea(self, image: List[List[str]], x: int, y: int) -> int:
        m, n = len(image), len(image[0])
        box_top, box_bottom = float('inf'), float('-inf')
        box_left, box_right = float('inf'), float('-inf')
 
        for r, row in enumerate(image):
            ends = self.find_row_ones(row)
            # No ones in the row
            if not ends:
                continue
            
            row_left, row_right = ends
            box_left, box_right = min(box_left, row_left), max(box_right, row_right)
            box_top, box_bottom = min(box_top, r), max(box_bottom, r)
 
        width = box_right - box_left + 1
        height = box_bottom - box_top + 1
        return width * height

DFS from source

Since a black pixel’s coordinates, , are already given, we can perform one DFS to find the four boundaries: box_left, box_right, box_top, and box_bottom. However, for dense and large black regions like below, we shall end up taking time.

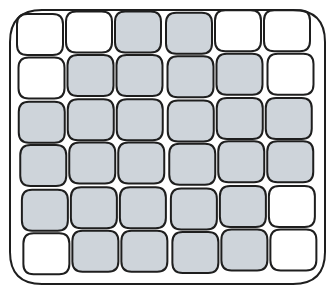
DFS along boundary

From the given black pixel , we can first do linear scan on the row and from there we can perform DFS only on the black pixels along the boundary to find extreme values of row and column which would give us the boundaries of the enclosing box. Although DFS along boundary is cheaper for dense black regions like above, it may end up taking time for regions like below:

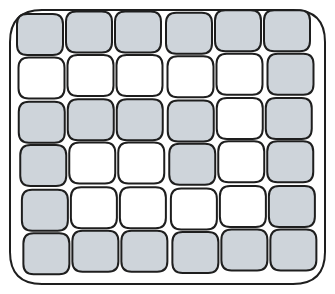
Expand from initial box

From the given black pixel, we can find an initial bounding box like below. The final bounding box, for the entire black region, must be at least as big as the initial box.

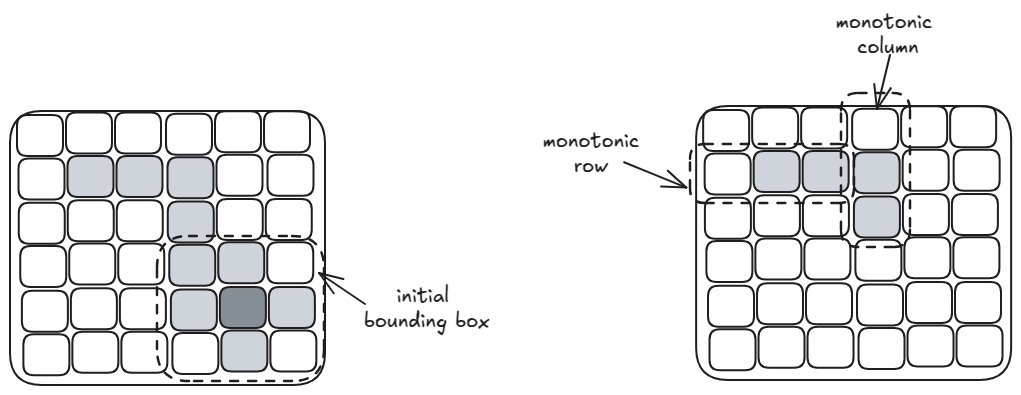
We also note that the parts above and left of this initial bounding box that could extend the enclosing box look monotonic — 0’s and 1’s are separated out. So, we could try binary search (from each row and each column) to find the furthest black pixels that can expand our initial box. The time complexity would be . However, the monotonic nature of these extensions are not guaranteed. An example is below:

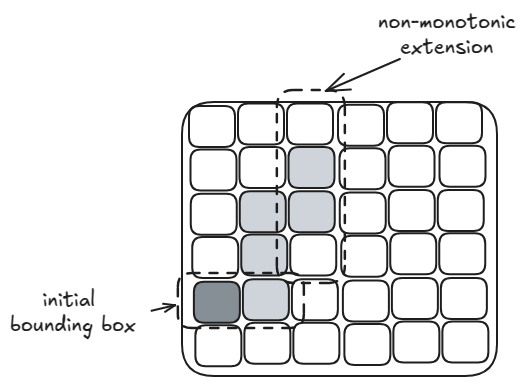
Binary search per row and column

Like the intermediate value theorem of a continuous function, for a connected black region, no matter its shape, if two different columns each has black pixel then all columns in between them must have black pixels. Likewise, if a column does not have a black pixel then the entire black region is either to its left or to its right. In other words, if we look from below, we see a connected black line.

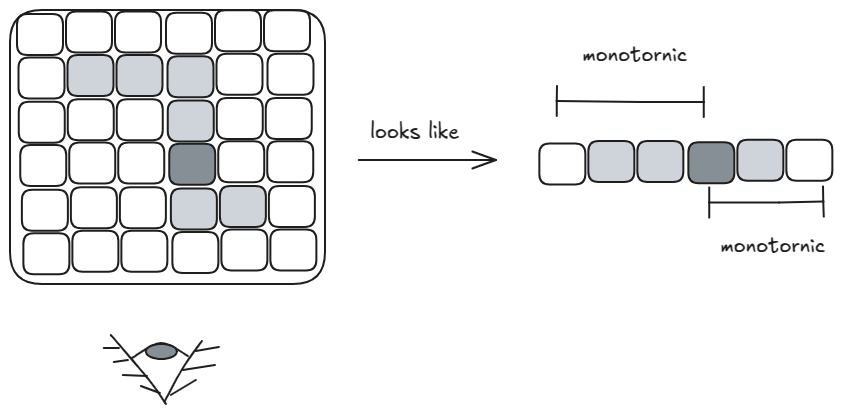
Starting at the given black pixel’s column, to its right, for each column, if we keep asking: “Does any row have a black pixel?”, we get a step-function-like sequence of answers: . This also holds for the columns to the left of the initial back pixel’s column.

From the side-view, for each row if we ask: “Does any column has a back pixel?”, we find similar monotonicity above and below the initial black pixel’s row.

This suggests binary-search to the left, right, above, and below the initial black pixel.

Time: , space: .

class Solution:
    def is_black_column(self, col, image) -> bool:
        return any(
            image[row][col] == "1" for row in range( len(image) )
        )
    
    def is_white_column(self, col, image) -> bool:
        return not self.is_black_column(col, image)

    def is_black_row(self, row, image) -> bool:
        return "1" in image[row]

    def is_white_row(self, row, image) -> bool:
        return not self.is_black_row(row, image)

    def find_leftmost(self, lo, hi, image, has_expected_color) -> int:
        while lo <= hi:
            mid = (lo+hi) // 2
            if has_expected_color(mid, image):
                hi = mid - 1
            else:
                lo = mid + 1

        return lo

    def minArea(self, image: List[List[str]], x: int, y: int) -> int:
        m, n = len(image), len(image[0])

        box_left = self.find_leftmost(
            0, y, image, self.is_black_column
        )

        box_right = self.find_leftmost(
            y+1, n-1, image, self.is_white_column
        ) - 1

        box_top = self.find_leftmost(
            0, x, image, self.is_black_row
        )

        box_bottom = self.find_leftmost(
            x+1, m-1, image, self.is_white_row
        ) - 1

        box_width = box_right - box_left + 1
        box_height = box_bottom - box_top + 1

        return box_width * box_height