We simulate continuous spiral motion defined by directions and their boundaries. To get the matrix filled up, we piggyback on this motion by hopping in and hopping out at the right times.
We hop in at while the motion has just moved from
Up -> Right, with Up’s boundary changed from row_min = 0 to row_min = 1. We hop out when we have copied all elements.
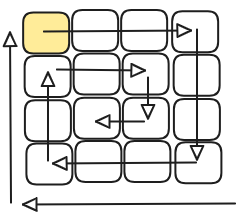
Time: , space:
.
from enum import Enum
class Dir(Enum):
Right = (0, 1)
Down = (1, 0)
Left = (0, -1)
Up = (-1, 0)
class Solution:
def is_invalid_move(
self, r, c, curr_dir, row_min, row_max, col_min, col_max
) -> bool:
match curr_dir:
case Dir.Right:
return c > col_max
case Dir.Down:
return r > row_max
case Dir.Left:
return c < col_min
case Dir.Up:
return r < row_min
def updated_boundaries(
self, curr_dir, row_min, row_max, col_min, col_max
) -> Tuple[int]:
match curr_dir:
case Dir.Right:
return (row_min, row_max, col_min, col_max - 1)
case Dir.Down:
return (row_min, row_max - 1, col_min, col_max)
case Dir.Left:
return (row_min, row_max, col_min + 1, col_max)
case Dir.Up:
return (row_min + 1, row_max, col_min, col_max)
def generateMatrix(self, n: int) -> List[List[int]]:
last_num = n * n
mat = [[0] * n for _ in range(n)]
next_dir = {
Dir.Right: Dir.Down,
Dir.Down: Dir.Left,
Dir.Left: Dir.Up,
Dir.Up: Dir.Right,
}
row_min, row_max = 0, n - 1
col_min, col_max = 0, n - 1
# Simulate continuous spiral motion
# Terminate based on external signal: count of elements
# Start with valid:
# - direction: Up -> Right
# - Up's boundary: row_min = 1
# - cell: (0, 0)
# - x: 1
r, c, curr_dir = 0, 0, Dir.Right
row_min += 1
x = 1
while x <= last_num:
mat[r][c] = x
x += 1
dr, dc = curr_dir.value
next_r, next_c = r + dr, c + dc
if self.is_invalid_move(
next_r, next_c, curr_dir, row_min, row_max, col_min, col_max
):
row_min, row_max, col_min, col_max = self.updated_boundaries(
curr_dir, row_min, row_max, col_min, col_max
)
curr_dir = next_dir[curr_dir]
dr, dc = curr_dir.value
next_r, next_c = r + dr, c + dc
r, c = next_r, next_c
return mat
Encapsulating spiral motion in a separate class makes the piggybacking explicit.
from enum import Enum
class Dir(Enum):
Right = (0, 1)
Down = (1, 0)
Left = (0, -1)
Up = (-1, 0)
class SpiralOrder:
next_dir = {
Dir.Right: Dir.Down,
Dir.Down: Dir.Left,
Dir.Left: Dir.Up,
Dir.Up: Dir.Right,
}
def __init__(self, n) -> None:
self.row_min, self.row_max = 0, n-1
self.col_min, self.col_max = 0, n-1
self.r, self.c = 0, -1
self.curr_dir = Dir.Up
def is_invalid_move(
self, dr, dc
) -> bool:
match self.curr_dir:
case Dir.Right:
return self.c+dc > self.col_max
case Dir.Down:
return self.r+dr > self.row_max
case Dir.Left:
return self.c+dc < self.col_min
case Dir.Up:
return self.r+dr < self.row_min
def update_boundaries(
self, curr_dir
) -> None:
match self.curr_dir:
case Dir.Right:
self.col_max -= 1
case Dir.Down:
self.row_max -= 1
case Dir.Left:
self.col_min += 1
case Dir.Up:
self.row_min += 1
def change_direction(self) -> None:
self.update_boundaries(self.curr_dir)
self.curr_dir = self.next_dir[self.curr_dir]
def __iter__(self):
return self
def __next__(self) -> Tuple[int]:
# No new cell to move to
if self.row_min > self.row_max or self.col_min > self.col_max:
return self.r, self.c
dr, dc = self.curr_dir.value
if self.is_invalid_move(dr, dc):
self.change_direction()
dr, dc = self.curr_dir.value
self.r, self.c = self.r + dr, self.c + dc
return self.r, self.c
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
mat = [[0] * n for _ in range(n)]
x = 1
last_num = n * n
for r, c in SpiralOrder(n):
if x > last_num:
break
mat[r][c] = x
x += 1
return mat
Leave a comment