Brute force
For each day we can scan into the future and pick the first day with a higher temperature. Time: .
Stack
If the temperatures are sorted in non-increasing order, no days will have a warmer day in the future. So, if any day has a future warmer day, there must be two consecutive days where temperature increases. Say, -th is the leftmost day where
. We can then use
-th day as the solution for
-th day. Since,
have non-increasing temperatures, the
-th day cannot be warmer day for any of
-th day. Removing
-th day, we now have a smaller problem involving the days:
.
In this smaller problem, the leftmost increasing pair is either or it lies in the range
. If
, we have again solved
-th day and have an even smaller problem to solve. Otherwise, the warmer days all are in the range
. Note, while we are considering
as a potential warmer day, we always look at the unsolved day immediately to its left. So, we use a stack.
Nesting
Another way to think is, say for the -th day, the earliest warmer day is the
-th day. Then the solutions between these two days are nested like below examples:
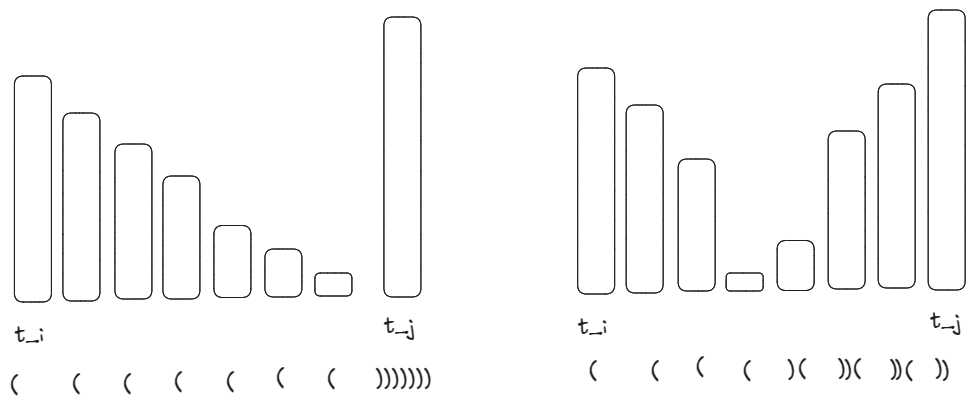
Time: , space:
class Solution:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
n = len(temperatures)
waits = [0] * n
stack = []
for i, curr_temp in enumerate(temperatures):
while stack and curr_temp > temperatures[top := stack[-1]]:
waits[top] = i - top
stack.pop()
stack.append(i)
return waits
Leave a comment