LeetCode 2077: Paths in Maze That Lead to Same Room

Backtrack

A 3-cycle like below consists of a 3-room path ( $\langle u \rightarrow v \rightarrow w \rangle$ ) and an edge from the last room to the first room ( $w \rightarrow u$ ).

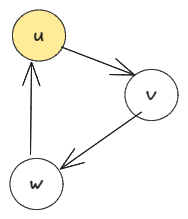
So, we consider each room as the head of a possible 3-cycle, generate 3-length path and check if there is an edge from last room to first.

If largest number of corridors from a room is $m$ , time: $\mathcal{O}(n \cdot m^3)$ , space, that of adjacency list: $\mathcal{O}(n \cdot m)$ .

class Solution:
    def get_adj_list(self, n, corridors) -> Dict[int, Set[int]]:
        adj_list = { u: set() for u in range(1, n+1) }
        for u, v in corridors:
            adj_list[u].add(v)
            adj_list[v].add(u)
        return adj_list

    def explore(self, adj_list, path, visited, cycles):
        if len(path) == 3:
            if path[0] in adj_list[path[-1]]:
                cycles.add( tuple( sorted(path) ) )
            return
        
        for v in adj_list[ path[-1] ]:
            if v in visited:
                continue
            visited.add(v)
            self.explore(adj_list, path+[v], visited, cycles)
            visited.remove(v)

    def numberOfPaths(self, n: int, corridors: List[List[int]]) -> int:
        adj_list = self.get_adj_list(n, corridors)
        cycles = set()
        for u in range(1, n+1):
            self.explore(adj_list, [u], {u}, cycles)
        return len(cycles)

Check all possible 3-rooms

Generate all ${n}\choose{3}$ groups of three rooms and check if they are in a cycle.

Time: $\mathcal{O}(n^3)$ , space is for adjacency list: $\mathcal{O}(n \cdot m)$ .

class Solution:
    def get_adj_list(self, n, corridors) -> Dict[int, Set[int]]:
        adj_list = { u: set() for u in range(1, n+1) }
        for u, v in corridors:
            adj_list[u].add(v)
            adj_list[v].add(u)
        return adj_list

    def numberOfPaths(self, n: int, corridors: List[List[int]]) -> int:
        adj_list = self.get_adj_list(n, corridors)
        count = 0
        for u in range(1, n+1):
            if not adj_list[u]:
                continue
            for v in range(u+1, n+1):
                if not adj_list[v] or v not in adj_list[u]:
                    continue
                for w in range(v+1, n+1):
                    if not adj_list[w] or w not in adj_list[v]:
                        continue
                    if u in adj_list[w]:
                        count += 1
        return count

Find third member per edge

For an edge $u \rightarrow v$ , we need a $w$ that is adjacent to both $u$ and $v$ , so we can take the intersection of the $u$ ‘s edge-set and $v$ ‘s edge-set.

If there are total $c$ corridors, time: $\mathcal{O}(c \cdot m)$ . Space, for adjacency list, $\mathcal{O}(n \cdot m)$ .

class Solution:
    def get_adj_list(self, n, corridors) -> Dict[int, Set[int]]:
        adj_list = { u: set() for u in range(1, n+1) }
        for u, v in corridors:
            adj_list[u].add(v)
            adj_list[v].add(u)
        return adj_list

    def numberOfPaths(self, n: int, corridors: List[List[int]]) -> int:
        adj_list = self.get_adj_list(n, corridors)
        cycles = set()
        for u, v in corridors:
            ws = adj_list[u] & adj_list[v]
            for w in ws:
                cycles.add( tuple( sorted([u, v, w]) ) )
        return len(cycles)

If we take the intersection as we are building the adjacency list, a cycle will be counted once when we consider the third edge, so we do not need to de-duplicate.

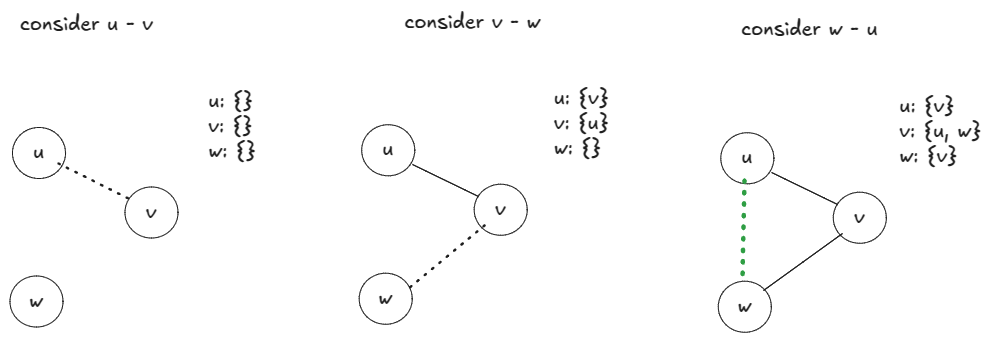
class Solution:
    def numberOfPaths(self, n: int, corridors: List[List[int]]) -> int:
        adj_list = {u: set() for u in range(1, n+1)}
        count = 0
        for u, v in corridors:
            adj_list[u].add(v)
            adj_list[v].add(u)
            count += len(adj_list[u] & adj_list[v])
        return count

unreasonably effective