LeetCode 332: Reconstruct Itinerary

Backtrack

A valid itinerary uses each ticket exactly once and is lexicographically sorted. So, we build a directed graph where an edge is a ticket. Starting with "JFK" we backtrack to find a path that consumes all tickets. Each hop of the path consumes one available ticket. We use sorted edge-lists so that possible next hops are considered in lexicographic order.

Say there are $n$ tickets. If the average size of a group of tickets with the same from is $m$ , then there are $k = \frac{n}{m}$ such groups. Time: $\mathcal{O}((m!)^k)$ , space: $\mathcal{O}(n)$ .

class Solution:
    def get_adj_list(self, tickets) -> Tuple[Dict[str, List[str]], Dict[Tuple[str], int]]:
        adj_list = {}
        available_tickets = {}
        for u, v in tickets:
            adj_list[u] = adj_list.get(u, []) + [v]
            available_tickets[(u, v)] = available_tickets.get((u, v), 0) + 1
        for u, edges in adj_list.items():
            adj_list[u] = sorted(edges)
        return adj_list, available_tickets

    def backtrack(self, u, adj_list, available_tickets, itinerary) -> List[str]:
        if not available_tickets:
            return itinerary
            
        for v in adj_list.get(u, []):
            ticket = (u, v)
            if ticket not in available_tickets:
                continue

            available_tickets[ticket] -= 1
            if available_tickets[ticket] == 0:
                del available_tickets[ticket]

            valid_itinerary = self.backtrack(v, adj_list, available_tickets, itinerary+[v])
            if valid_itinerary:
                return valid_itinerary

            available_tickets[ticket] = available_tickets.get(ticket, 0) + 1

    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        n = len(tickets)
        adj_list, available_tickets = self.get_adj_list(tickets)
        return self.backtrack("JFK", adj_list, available_tickets, ["JFK"])

Hierholzer’s for Eulerian path

For any directed graph, there is an underlying DAG whose vertices are strongly connected components (SCC) of the original graph.

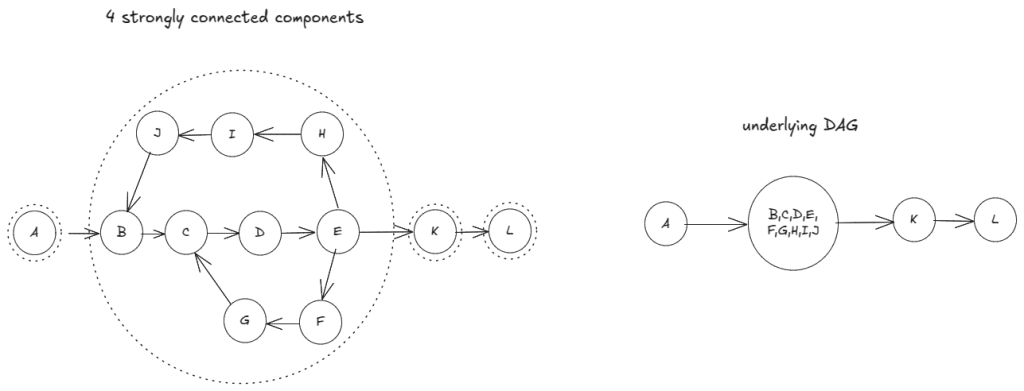
A source (A) to sink (L) path that visits all edges (not necessarily exactly once) must visit the SCCs in a topological order of the underlying DAG. That means, in topological order, we need to finish visiting first SCC completely, then move onto the second SCC and so on. How could we process an SCC without spilling over to another? Say we want to visit only the largest SCC above. If we start at $\textcircled{H}$ , it is not possible to spill over to an earlier SCC like $\textcircled{A}$ , but a DFS will spill over to a later SCC like $\textcircled{K}$ . So, the visit would not be contained within a single SCC. However, if we start at any node within the sink SCC like $\textcircled{L}$ , the visit will remain contained within the sink SCC. So, we could process the SCCs in sink-to-source order and then reverse to get the path.

Itinerary is an Eulerian path. The existence of an Eulerian path makes each SCC special. Here, an SCC is either a single node or some loops that starts and ends at the same vertex. Because, except for the start and end vertices, all other vertices must have same out-degree and in-degree — we should be able to exit the node same number of times as we enter it. The earlier graph does not have an Eulerian path. But we can modify it to have an Eulerian path like below.

If there is an Eulerian path, no loops within an SCC share an edge. We can process each loop once and be done with all edges of that loop. Due to this non-overlapping loop structure, within an SCC we do not visit an edge more than once. To find an Eulerian path, the overall strategy is then:

Find sink-to-source order of SCCs.
- Use DFS forward pass to reach sink SCC. We remove an edge as soon as we visit. This forms a backbone path (in the recursion stack) that connects the SCCs.
Within an SCC, if a vertex ( for example) has multiple outgoing edges, take one of these edges (in any order) and be done with all edges until we circle back to . Then, pick next remaining outgoing edge of and so on. When there are no more outgoing edges, we are done with the SCC containing . Now move on to the earlier SCC, .
- In reverse path of DFS, process each vertex until there are no more edges, essentially processing SCCs in sink-to-source order.
In the end, reverse the found path, so we respect the underlying DAG’s source-to-sink order.

This is Hierholzer’s algorithm. Our itinerary or Eulerian path must also be lexicographically sorted. So, for a vertex, we always pick the outgoing edges in reverse lexicographic order to make sure when we do the reversing in step 3, we end up with lexicographic order.

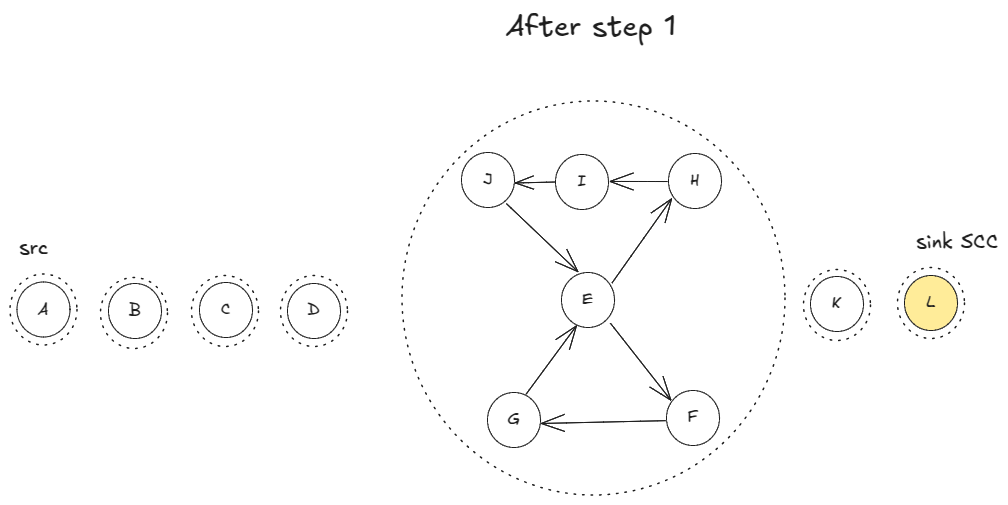
The earlier graph, after step 1, looks like below:

The rest of the steps:

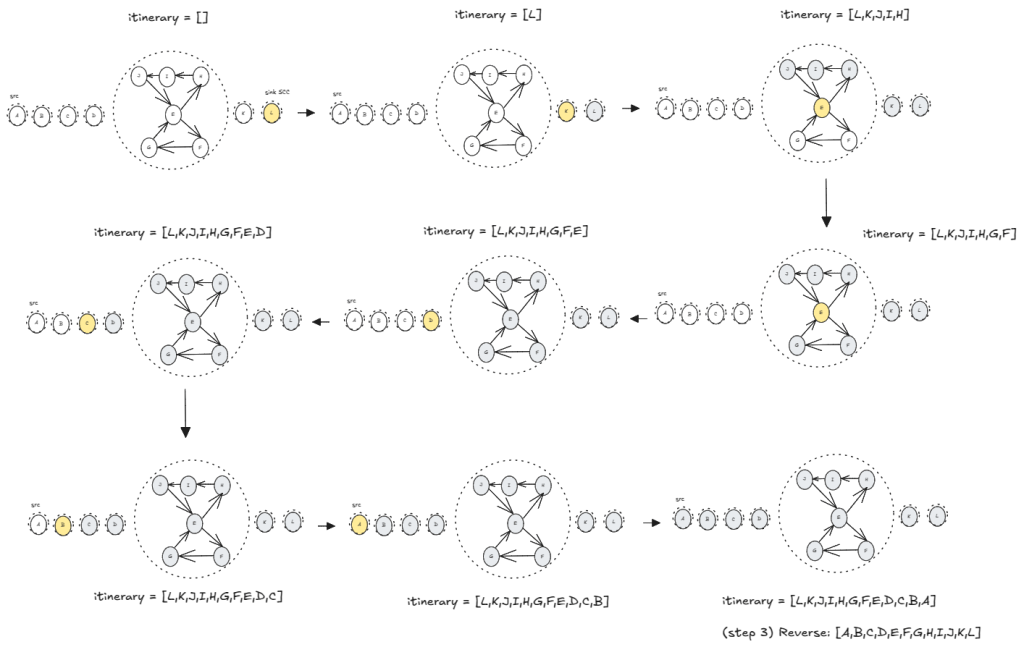
Time: $\mathcal{O}(n + k \cdot \lg{m})$ , space for adjacency list: $\mathcal{O}(n)$ .

class Solution:
    def get_adj_list(self, tickets) -> Dict[int, List[int]]:
        adj_list = {}
        for u, v in tickets:
            adj_list[u] = adj_list.get(u, []) + [v]
        # Sort in reverse so final reverse restores lexicographic order
        [edges.sort(reverse=True) for edges in adj_list.values()]
        return adj_list

    def dfs(self, u, adj_list, itinerary) -> None:
        while edges := adj_list.get(u, []):
            v = edges.pop()
            self.dfs(v, adj_list, itinerary)
        # SCC containing u is done
        itinerary.append(u)

    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        adj_list = self.get_adj_list(tickets)
        itinerary = []
        self.dfs("JFK", adj_list, itinerary)
        return itinerary[::-1]

With explicit stack we could find itinerary iteratively:

class Solution:
    def get_adj_list(self, tickets) -> Dict[int, List[int]]:
        adj_list = {}
        for u, v in tickets:
            adj_list[u] = adj_list.get(u, []) + [v]
        # Sort in reverse so final reverse restores lexicographic order
        [edges.sort(reverse=True) for edges in adj_list.values()]
        return adj_list

    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        adj_list = self.get_adj_list(tickets)
        itinerary = []
        stack = ["JFK"]
        while stack:
            u = stack[-1]
            if edges := adj_list.get(u, []):
                v = edges.pop()
                stack.append(v)
            else:
                # SCC containing u is done
                itinerary.append(stack.pop())
        return itinerary[::-1]

unreasonably effective