LeetCode 114: Flatten Binary Tree to Linked List

Recursive

A flattened list has a head and a tail. We recursively flatten root.left and root.right and then combine the flattened sublists to build a longer list: root -> flattened_left -> flattened_right.

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}( \texttt{tree-height} )$

class Solution:
    def dfs(self, root) -> Tuple[TreeNode, TreeNode]:
        if not root:
            return None, None

        left_head, left_tail = self.dfs(root.left)
        right_head, right_tail = self.dfs(root.right)
        root.left = None

        head = root
        tail = right_tail or left_tail or root
        
        if left_head and right_head:
            left_tail.right = right_head
            root.right = left_head
        elif left_head:
            root.right = left_head
        
        return head, tail

    def flatten(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        self.dfs(root)

Root becomes the head of the flattened list, so we do not need to keep track of head of the list, only tail is sufficient.

class Solution:
    def dfs(self, root) -> TreeNode:
        if not root:
            return None

        left_tail = self.dfs(root.left)
        right_tail = self.dfs(root.right)

        if left_tail:
            left_tail.right = root.right
            root.right = root.left
            root.left = None

        return right_tail or left_tail or root

    def flatten(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        self.dfs(root)

We can flatten the tree without a helper function, in-place.

class Solution:
    def flatten(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        if not root:
            return None

        self.flatten(root.left)
        self.flatten(root.right)

        flattened_right = root.right
        root.right = root.left
        root.left = None
        
        # Find right of flattened left
        while root.right:
            root = root.right
        root.right = flattened_right

Iterative

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}( \texttt{tree-height} )$ .

class Solution:
    def flatten(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        if not root:
            return None
        stack = [root]
        while stack:
            u = stack.pop()
            [stack.append(c) for c in (u.right, u.left) if c]
            # Link to successor
            u.right = stack[-1] if stack else None
            u.left = None

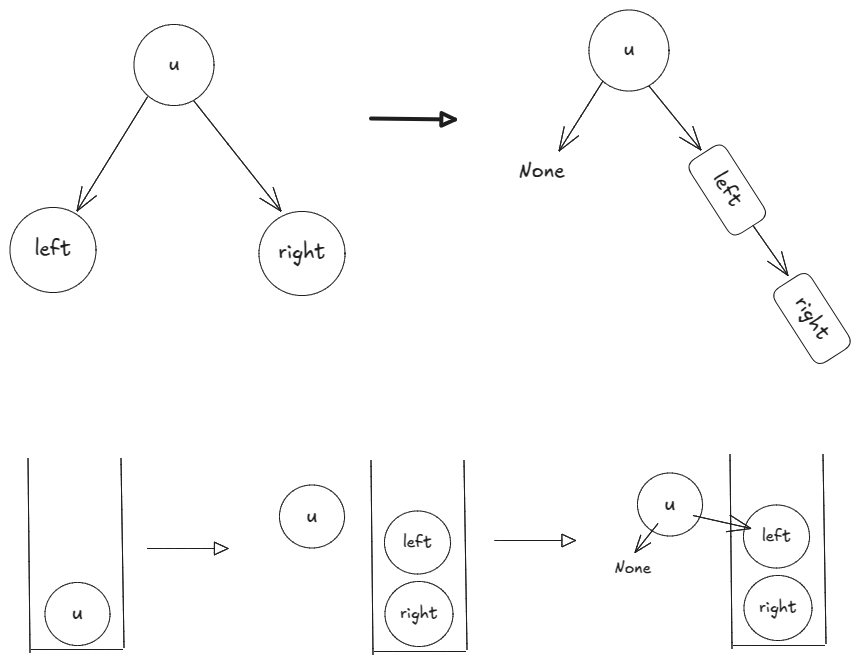
With implicit or explicit stack, we are keeping track of the root until the left subtree is flattened. Then we move the flattened left subtree to the right of root.

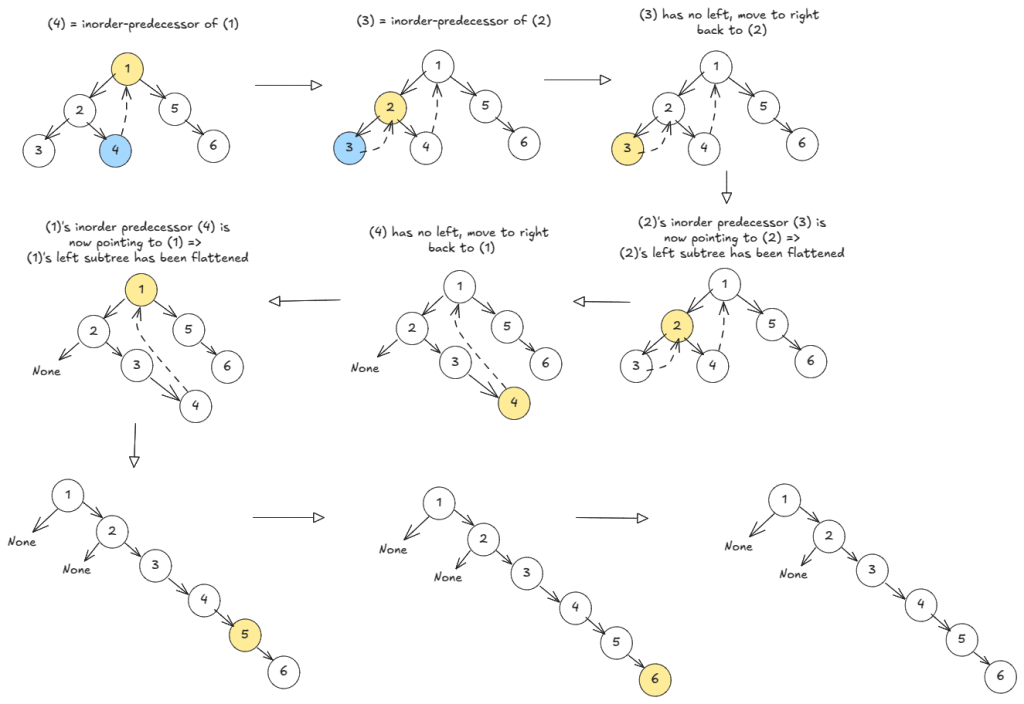
Instead, we could find the left subtree’s last node (inorder predecessor of root) that will be visited during flattening and link it to the root. Now we could move onto the left subtree of root. Because, once the left subtree is flattened, root will sit next to its inorder predecessor. This is Morris traversal.

Time: $\mathcal{O}(2 \cdot n) = \mathcal{O}(n)$ , space: $\mathcal{O}(1)$ .

class Solution:
    def flatten(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        while root:
            if not root.left:
                root = root.right
                continue

            pred = root.left
            while pred.right and pred.right != root:
                pred = pred.right

            if pred.right != root:
                # Link: (last node of left subtree) -> (current node)
                pred.right = root
                root = root.left
                continue

            # Left subtree has been flattened
            pred.right = None
            right_subtree = root.right
            root.right = root.left
            root.left = None
            pred.right = right_subtree
            root = pred.right

unreasonably effective