Recursive
A flattened list has a head and a tail. We recursively flatten root.left and root.right and then combine the flattened sublists to build a longer list: root -> flattened_left -> flattened_right.
Time: , space:
class Solution:
def dfs(self, root) -> Tuple[TreeNode, TreeNode]:
if not root:
return None, None
left_head, left_tail = self.dfs(root.left)
right_head, right_tail = self.dfs(root.right)
root.left = None
head = root
tail = right_tail or left_tail or root
if left_head and right_head:
left_tail.right = right_head
root.right = left_head
elif left_head:
root.right = left_head
return head, tail
def flatten(self, root: Optional[TreeNode]) -> None:
"""
Do not return anything, modify root in-place instead.
"""
self.dfs(root)
Root becomes the head of the flattened list, so we do not need to keep track of head of the list, only tail is sufficient.
class Solution:
def dfs(self, root) -> TreeNode:
if not root:
return None
left_tail = self.dfs(root.left)
right_tail = self.dfs(root.right)
if left_tail:
left_tail.right = root.right
root.right = root.left
root.left = None
return right_tail or left_tail or root
def flatten(self, root: Optional[TreeNode]) -> None:
"""
Do not return anything, modify root in-place instead.
"""
self.dfs(root)
We can flatten the tree without a helper function, in-place.
class Solution:
def flatten(self, root: Optional[TreeNode]) -> None:
"""
Do not return anything, modify root in-place instead.
"""
if not root:
return None
self.flatten(root.left)
self.flatten(root.right)
flattened_right = root.right
root.right = root.left
root.left = None
# Find right of flattened left
while root.right:
root = root.right
root.right = flattened_right
Iterative
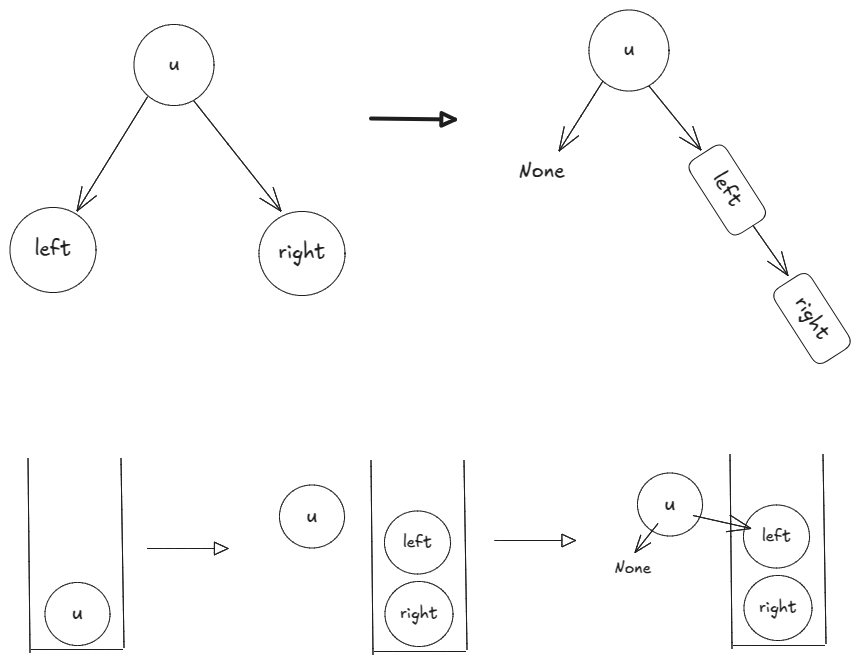
Time: , space:
.
class Solution:
def flatten(self, root: Optional[TreeNode]) -> None:
"""
Do not return anything, modify root in-place instead.
"""
if not root:
return None
stack = [root]
while stack:
u = stack.pop()
[stack.append(c) for c in (u.right, u.left) if c]
# Link to successor
u.right = stack[-1] if stack else None
u.left = None
With implicit or explicit stack, we are keeping track of the root until the left subtree is flattened. Then we move the flattened left subtree to the right of root.
Instead, we could find the left subtree’s last node (inorder predecessor of root) that will be visited during flattening and link it to the root. Now we could move onto the left subtree of root. Because, once the left subtree is flattened, root will sit next to its inorder predecessor. This is Morris traversal.
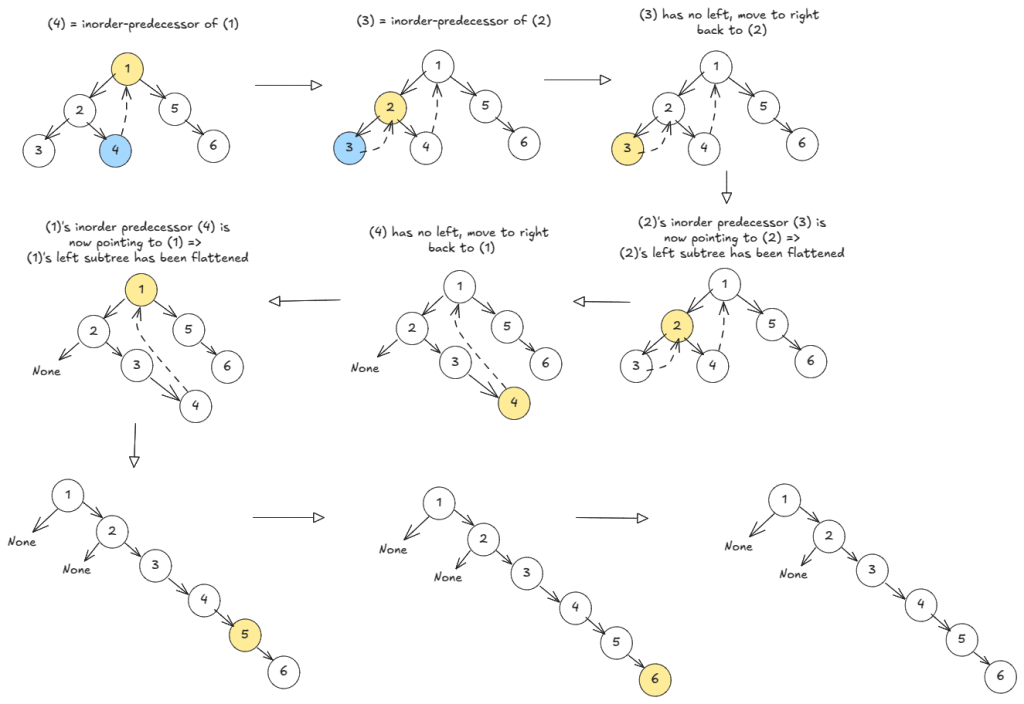
Time: , space:
.
class Solution:
def flatten(self, root: Optional[TreeNode]) -> None:
"""
Do not return anything, modify root in-place instead.
"""
while root:
if not root.left:
root = root.right
continue
pred = root.left
while pred.right and pred.right != root:
pred = pred.right
if pred.right != root:
# Link: (last node of left subtree) -> (current node)
pred.right = root
root = root.left
continue
# Left subtree has been flattened
pred.right = None
right_subtree = root.right
root.right = root.left
root.left = None
pred.right = right_subtree
root = pred.right
Leave a comment