LeetCode 1380: Lucky Numbers in a Matrix

link

A lucky number is both a row min and a column max. We find the row mins and column maxes in one pass and return their overlap as the lucky numbers.

Time: $\mathcal{O}(m \cdot n)$ , space: $\mathcal{O}(m+n)$ .

from itertools import product as cartesian

class Solution:
    def luckyNumbers(self, matrix: List[List[int]]) -> List[int]:
        m, n = len(matrix), len(matrix[0])
        row_min = [float("inf")] * m
        col_max = [float("-inf")] * n
        for r, c in cartesian(range(m), range(n)):
            row_min[r] = min( row_min[r], matrix[r][c] )
            col_max[c] = max( col_max[c], matrix[r][c] )
        overlap = set(row_min) & set(col_max)
        return list(overlap)

O(1) extra space: reuse matrix

If modifying the matrix is feasible, we could use the first row to save column maxes and first column to save row maxes. The extra space would be constant.

from itertools import product as cartesian

class Solution:
    def luckyNumbers(self, matrix: List[List[int]]) -> List[int]:
        m, n = len(matrix), len(matrix[0])
        first_row_min = min(matrix[0])
        first_col_max = float("-inf")
        for r in range(m):
            first_col_max = max(first_col_max, matrix[r][0])
        
        luckies = []
        if first_row_min == first_col_max:
            luckies.append(first_row_min)

        for r, c in cartesian(range(1, m), range(1, n)):
            matrix[r][0] = min( matrix[r][0], matrix[r][c] )
            matrix[0][c] = max( matrix[0][c], matrix[r][c] )

        for r in range(1, m):
            row_min = matrix[r][0]
            if row_min == first_col_max:
                luckies.append(row_min)
        for c in range(1, n):
            col_max = matrix[0][c]
            if col_max == first_row_min:
                luckies.append(col_max)
        
        for r, c in cartesian(range(1, m), range(1, n)):
            row_min = matrix[r][0]
            col_max = matrix[0][c]
            if row_min == col_max:
                luckies.append(row_min)
        
        return luckies

O(1) extra space: unique lucky number

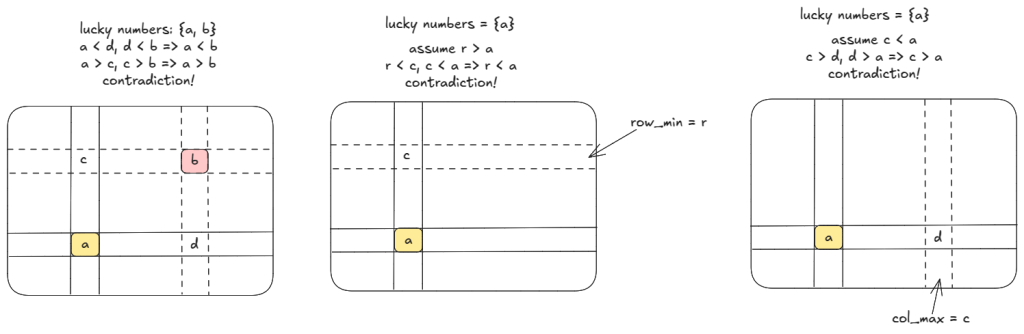
Observations about a lucky number:

A lucky number is the biggest row-min.
- Being the biggest in its column, a lucky number is bigger than at least one element on each row. So, it is bigger than mins on other rows.
- Consequently, there is a single row where a lucky number can appear.
A lucky number is the smallest col-max.
- Being the smallest in its row, a lucky number is smaller than at least one element in each column. So, it is smaller than maxes on other columns.
- Consequently, there is a single column where a lucky number can appear.

Above two implies, there can a single lucky number.

Time: $\mathcal{O}(m \cdot n)$ , space: $\mathcal{O}(1)$ .

class Solution:
    def luckyNumbers(self, matrix: List[List[int]]) -> List[int]:
        m, n = len(matrix), len(matrix[0])
        max_row_min = float("-inf")
        for row in matrix:
            max_row_min = max(max_row_min, min(row))
        min_col_max = float("inf")
        for c in range(n):
            min_col_max = min(min_col_max, max(matrix[r][c] for r in range(m)))
        return [max_row_min] if max_row_min == min_col_max else []

unreasonably effective