Special type of directed graph where a node can have at most two outgoing edges and one incoming edge. Unlike graphs, with a binary tree, we differentiate between the two outgoing edges by marking one as left and the other as right.
Test helpers
class TreeNode:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
def serialize(root) -> str:
if not root:
return ""
if not root.left and not root.right:
return root.val
left_child = serialize(root.left)
right_child = serialize(root.right)
return f"{root.val}({left_child})[{right_child}]"
def deserialize(data) -> TreeNode:
if not data:
return None
l = data.find("(")
if l < 0:
return TreeNode(int(data))
stack = []
val, sign = None, 1
for c in data:
if c.isdigit():
val = int(c) if val is None else 10*val + int(c)
elif c == "-":
sign = -1
elif c == "(":
if val is not None:
val = sign * val
stack.append(TreeNode(val))
val, sign = None, 1
stack.append(c)
elif c == "[":
stack.append(c)
else:
if val is not None:
val = sign * val
stack.append(TreeNode(val))
val, sign = None, 1
if stack[-1] == "(" or stack[-1] == "[":
stack.pop()
stack.append(None)
elif stack[-2] == "(" or stack[-2] == "[":
root = stack.pop()
stack.pop()
stack.append(root)
else:
right_child = stack.pop()
left_child = stack.pop()
root = stack.pop()
stack.pop()
root.left = left_child
root.right = right_child
stack.append(root)
right_child = stack.pop()
left_child = stack.pop()
root = stack.pop()
root.left = left_child
root.right = right_child
return root
Height
Height of a node :
Height is the count of edges along the longest path from root to a leaf.
def height(root) -> int:
def is_leaf(u):
return not (u.left or u.right)
if not root or is_leaf(root):
return 0
return max( height(root.left), height(root.right) ) + 1
def height_stack(root) -> int:
def is_leaf(u):
return not (u.left or u.right)
if not root or is_leaf(root):
return 0
height = 0
stack = [(root, 0)]
while stack:
u, h = stack.pop()
height = max(height, h)
stack.extend((c, h+1) for c in (u.left, u.right) if c)
return height
Using “Threaded Binary Tree”, we can traverse a tree using constant extra space. This is called Morris traversal.
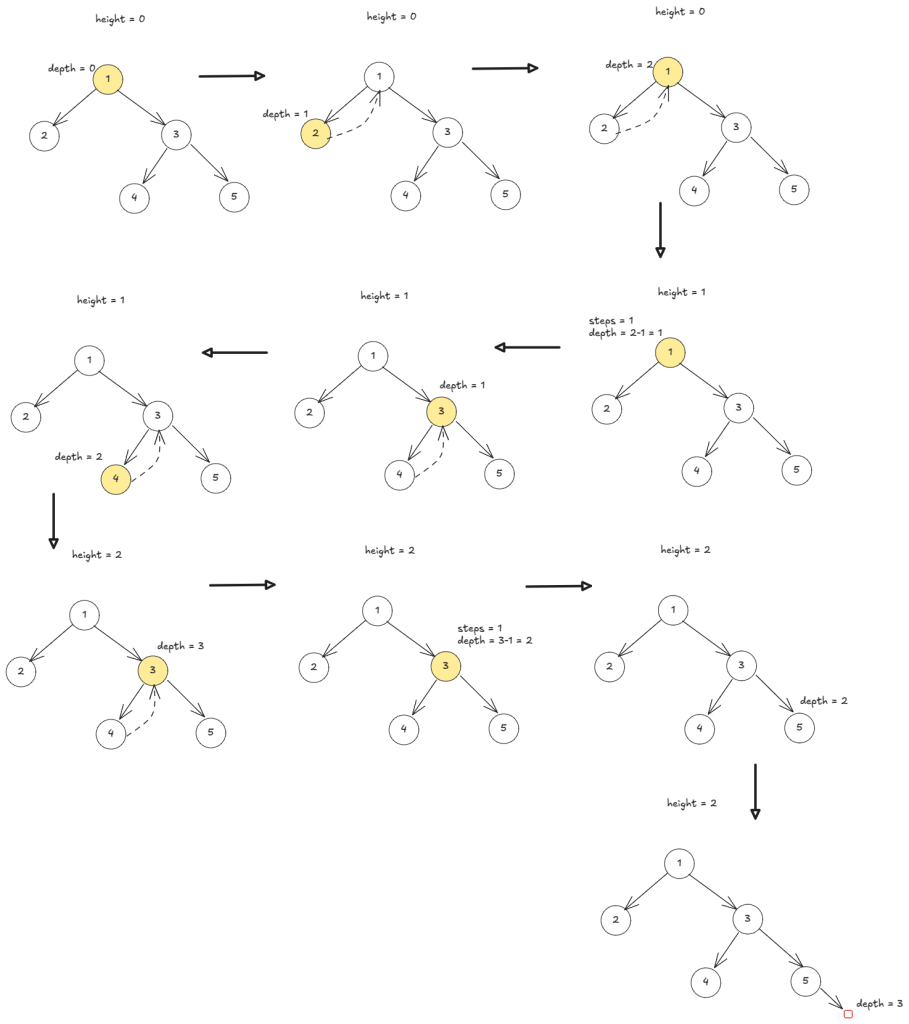
def height_morris(root) -> int:
depth, height = 0, 0
while root:
if not root.left:
root = root.right
depth += 1
height = max(height, depth-1)
continue
pred = root.left
steps = 1
while pred.right and pred.right != root:
pred = pred.right
steps += 1
if not pred.right:
pred.right = root
root = root.left
depth += 1
height = max(height, depth-1)
else:
pred.right = None
depth -= steps
root = root.right
return height
data = "1(2)[3(4)[5]]"
root = deserialize(data)
h, hs, hm = height(root), height_stack(root), height_morris(root)
print(f"{h=},{hs=},{hm=}")
data = "1()[2()[3]]"
root = deserialize(data)
h, hs, hm = height(root), height_stack(root), height_morris(root)
print(f"{h=},{hs=},{hm=}")
data = "1(2(3)[])[]"
root = deserialize(data)
h, hs, hm = height(root), height_stack(root), height_morris(root)
print(f"{h=},{hs=},{hm=}")
# h=2,hs=2,hm=2
# h=2,hs=2,hm=2
# h=2,hs=2,hm=2
Leave a comment