LeetCode 543: Diameter of Binary Tree

Recursive

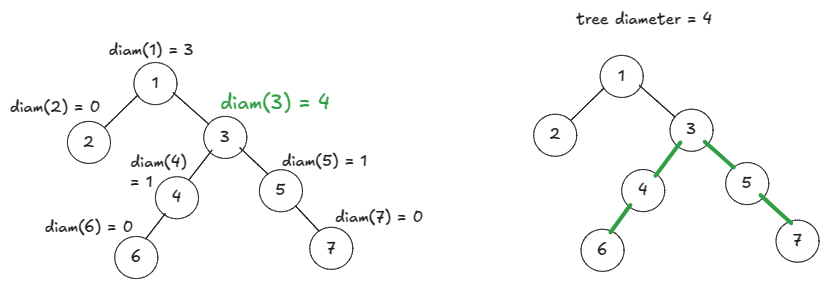
Diameter is the edge count along the longest path. The longest path going through a node can have parts from both left and right subtrees.

It is hard to define diameter going through a node in terms of diameter of its children. $\texttt{Diameter}(u) \stackrel{\text{\small ?}}{=} f\left( \texttt{Diameter}(u.left), \texttt{Diameter}(u.right) \right)$ .

However, it is easy to define $\texttt{Diameter}(u)$ in terms of height of $u$ ‘s children. $\texttt{Diameter}(u) = \texttt{Height}(u.left) + \texttt{Height}(u.right)$ . And, height of a node is easy to define recursively: $\texttt{Height}(v) = \max{\left( \texttt{Height}(v.left), \texttt{Height}(v.right) \right)} + 1$ .

So, we recursively find height of a node and piggyback on that recursion to compute the length of the longest path that goes through the node. Diameter of the tree is then the max such length.

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(\texttt{tree-height})$ .

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        max_diameter = float("-inf")
        def height(u: TreeNode) -> int:
            nonlocal max_diameter
            if not u:
                return 0
            left_height = height(u.left)
            right_height = height(u.right)
            diameter = left_height + right_height
            max_diameter = max(max_diameter, diameter)
            return max(left_height, right_height) + 1
        
        # Piggyback on height() recursion to compute diameter
        _ = height(root)
        return max_diameter

Iterative

The recursion unwinds first and does the computation on the return path, bottom-up. So, with an explicit stack and visited set, we do the unwinding and compute on the return path as well. For each node we keep its computed height in a dict. Second time we visit a node, it is in the return path, so by then height of its children have been computed and available in the dict.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        max_diameter = 0
        height = {}
        visited = set()
        stack = [root]
        while stack:
            top = stack.pop()
            if top not in visited:
                visited.add(top)
                stack.extend(u for u in (top, top.right, top.left) if u)
                continue

            # Return path, by now height of top's children have been computed
            left_height = height[top.left] if top.left else 0
            right_height = height[top.right] if top.right else 0
            height[top] = max( left_height, right_height ) + 1
            diameter = left_height + right_height
            max_diameter = max( max_diameter, diameter )

        return max_diameter

unreasonably effective