LeetCode 124: Binary Tree Maximum Path Sum

Recursive

In the binary tree, there are two types of path: (1) linear (2) curved. Sum on a linear path may contribute to parent’s sum. Sum on a curved path does not contribute to parent’s sum.

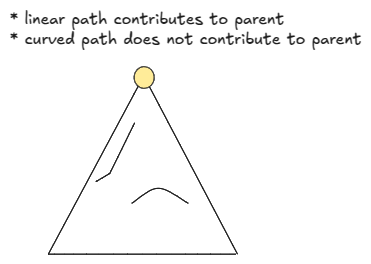
Say $L(u)$ is the linear sum of the node $u$ — sum on a linear path that ends at $u$ . So, $L(u)$ must include $u.val$ but including $L(u.left)$ or $L(u.right)$ is optional.

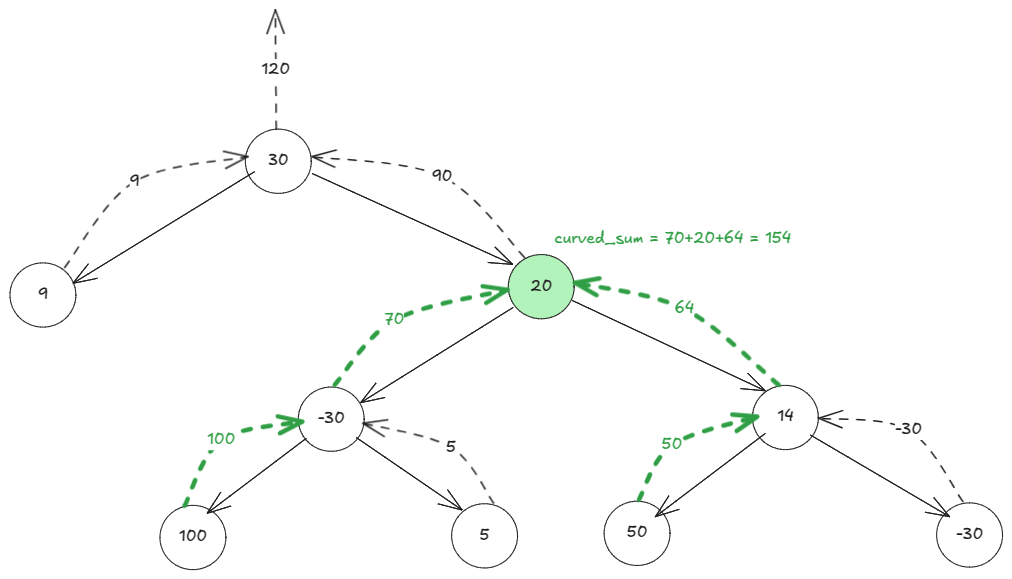
$L(u) = \begin{cases} 0, & \text{if } u \text{ is } \text{None} \\ \max{ \left( u.val, \max{\left( L(u.left), L(u.right) \right)} + u.val \right) } & \text{otherwise} \end{cases}$

On the other hand, if $C(u)$ is the curved sum:

$C(u) = \begin{cases} 0, & \text{if } u \text{ is } \text{None} \\ L(u.left) + u.val + L(u.right) & \text{otherwise} \end{cases}$

Then the max path sum of the tree is $\max_{u \in \texttt{tree}}{ \left( L(u), C(u) \right) }$ .

We recursively compute $L(u)$ keeping track of max $L(u)$ bottom-up. For $C(u)$ we piggyback on the same recursion.

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(\texttt{tree-height})$ .

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        max_curved_sum = float("-inf")
        max_linear_sum = float("-inf")
        
        def compute_linear_sum(u) -> int:
            nonlocal max_curved_sum, max_linear_sum
            if not u:
                return 0
            left_linear_sum = compute_linear_sum(u.left)
            right_linear_sum = compute_linear_sum(u.right)
            max_child_linear_sum = max( left_linear_sum, right_linear_sum )
            
            linear_sum = max( max_child_linear_sum+u.val, u.val )
            max_linear_sum = max( max_linear_sum, linear_sum )
            
            curved_sum = left_linear_sum + u.val + right_linear_sum
            max_curved_sum = max( max_curved_sum, curved_sum )

            return linear_sum

        _ = compute_linear_sum(root)
        return max(max_curved_sum, max_linear_sum)

Iterative

With explicit stack we simulate the bottom-up recursion using visited set and linear_sums dict. Second time we visit a node, on the return path, the linear sums of its children have already been computed.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0

        max_curved_sum = float("-inf")
        max_linear_sum = float("-inf")

        visited = set()
        linear_sums = {}
        stack = [root]
        while stack:
            u = stack.pop()
            
            if u not in visited:
                visited.add(u)
                stack.extend( v for v in (u, u.left, u.right) if v )
                continue
            
            # Return path: linear sums of u's children are available
            left_linear_sum = linear_sums[u.left] if u.left else 0
            right_linear_sum = linear_sums[u.right] if u.right else 0
            max_child_linear_sum = max( left_linear_sum, right_linear_sum )

            linear_sum = max( u.val, max_child_linear_sum + u.val )
            linear_sums[u] = linear_sum
            max_linear_sum = max( max_linear_sum, linear_sum )

            curved_sum = left_linear_sum + u.val + right_linear_sum
            max_curved_sum = max( max_curved_sum, curved_sum )
        
        return max( max_curved_sum, max_linear_sum )

unreasonably effective