LeetCode 105: Construct Binary Tree from Preorder and Inorder Traversal

Recursive

We want to formulate the problem recursively:

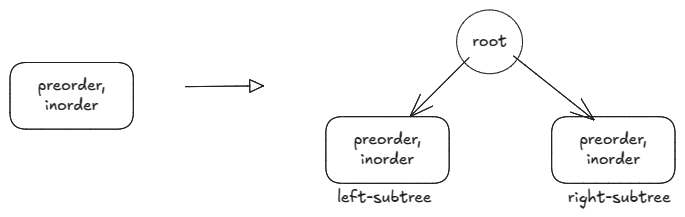
From preorder we know val of root. Since values are distinct, we can find the inorder position of the root’s val and that gives us lengths of left and right subtrees. From the subtree lengths and root’s position, now we know the (start, end) indices of left and right subtrees in both preorder and inorder. We recursively solve them. To efficiently find the inorder position of root’s val, we create a dict: {inorder-val -> inorder-position}.

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(n)$ .

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def make_tree(
        self, pre_lo, pre_hi, preorder, in_lo, in_hi, inorder, in_map
    ) -> Optional[TreeNode]:
        if pre_lo > pre_hi:
            return None
        root_val = preorder[pre_lo]
        root = TreeNode(int(root_val))
        
        root_pos = in_map[root_val]
        left_length = root_pos - in_lo
        right_length = in_hi - root_pos

        left_pre_lo = pre_lo + 1
        left_pre_hi = left_pre_lo + left_length - 1
        left_in_lo = in_lo
        left_in_hi = root_pos - 1

        root.left = self.make_tree(
            left_pre_lo, left_pre_hi, preorder, left_in_lo, left_in_hi, inorder, in_map
        )

        right_pre_lo = left_pre_hi + 1
        right_pre_hi = pre_hi
        right_in_lo = root_pos + 1
        right_in_hi = in_hi

        root.right = self.make_tree(
            right_pre_lo,
            right_pre_hi,
            preorder,
            right_in_lo,
            right_in_hi,
            inorder,
            in_map,
        )
        
        return root

    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        in_map = {x: i for i, x in enumerate(inorder)}
        return self.make_tree(
            0, len(preorder) - 1, preorder, 0, len(inorder) - 1, inorder, in_map
        )

Iterative

With an explicit stack we simulate the bottom up recursion using visited set and nodes dict. Second time we visit a node, on the return path, the TreeNode‘s of the children ranges are available.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        def get_subtrees(root, in_map) -> Tuple[Tuple[int]]:
            pre_lo, pre_hi, in_lo, in_hi = root
            root_pos = in_map[ preorder[pre_lo] ]
            left_len = root_pos - in_lo
            right_len = in_hi - root_pos

            left_pre_lo = pre_lo+1
            left_pre_hi = left_pre_lo+left_len-1
            left_in_lo = in_lo
            left_in_hi = root_pos-1
            left_subtree = (left_pre_lo, left_pre_hi, left_in_lo, left_in_hi)

            right_pre_lo = left_pre_hi+1
            right_pre_hi = pre_hi
            right_in_lo = root_pos+1
            right_in_hi = in_hi
            right_subtree = (right_pre_lo, right_pre_hi, right_in_lo, right_in_hi)

            return left_subtree, right_subtree

        if not preorder:
            return None

        in_map = {x: i for i, x in enumerate(inorder)}

        visited = set()
        nodes = {}
        root = (0, len(preorder)-1, 0, len(inorder)-1)
        stack = [root]
        while stack:
            u = stack.pop()
            if u not in visited:
                visited.add(u)
                left_subtree, right_subtree = get_subtrees(u, in_map)
                stack.extend(v for v in (u, left_subtree, right_subtree) if v[0] <= v[1])
                continue
        
            # Return path: u's children are available
            pre_lo, *_ = u
            u_node = TreeNode(preorder[pre_lo])
            left_subtree, right_subtree = get_subtrees(u, in_map)
            u_node.left = nodes.get(left_subtree, None)
            u_node.right = nodes.get(right_subtree, None)
            nodes[u] = u_node

        return nodes[root]

unreasonably effective