LeetCode 285: Inorder Successor in BST

Recursive

If we traverse the tree inorder, then the inorder successor of $p$ will be visited right after $p$ . So, during inorder traversal, we return the first node after the event $\texttt{root} = p$ .

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(\texttt{tree-height})$ .

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def inorderSuccessor(self, root: TreeNode, p: TreeNode) -> Optional[TreeNode]:
        p_found = False
        def inorder(root: TreeNode, p: TreeNode) -> Optional[TreeNode]:
            nonlocal p_found

            if not root:
                return None

            if succ := inorder(root.left, p):
                return succ

            if p_found:
                return root
            p_found = (root == p)

            if succ := inorder(root.right, p):
                return succ
            
        return inorder(root, p)

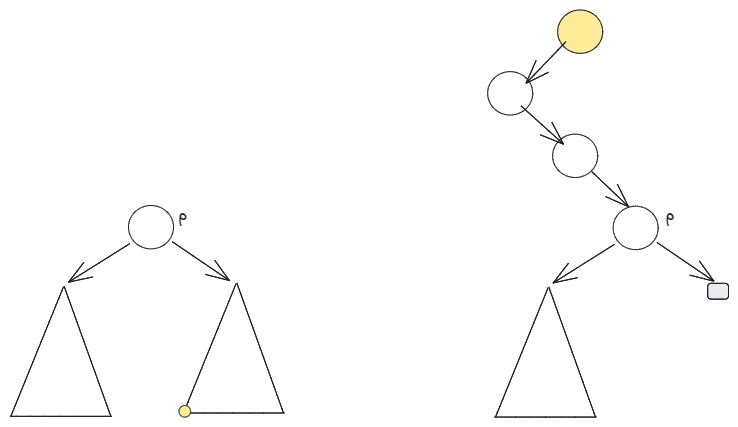
The above approach works for any binary tree. Since we have a BST, we can do better.

If $p$ has a right subtree, then $p$ ‘s inorder successor is the node with the smallest value in the right subtree which is either $p$ ‘s right child or the leftmost child of the right child.

If $p$ does not have a right subtree, the inorder successor is the lowest ancestor of $p$ whose left subtree contains $p$ .

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None


class Solution:
    def inorderSuccessor(self, root: TreeNode, p: TreeNode) -> Optional[TreeNode]:
        def find_ancestor_successor(root, is_left_child, parent, p):
            if root == p:
                return parent if is_left_child else None

            if p.val < root.val and (
                succ := find_ancestor_successor(root.left, True, root, p)
            ):
                return succ
            if p.val > root.val and (
                succ := find_ancestor_successor(root.right, False, root, p)
            ):
                return succ

            return parent if is_left_child else None

        if not p.right:
            return find_ancestor_successor(root, True, None, p)
            
        succ = p.right
        while succ.left:
            succ = succ.left
        return succ

Iterative

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(1)$ .

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None


class Solution:
    def inorderSuccessor(self, root: TreeNode, p: TreeNode) -> Optional[TreeNode]:
        def find_descendant_succ(root):
            succ = root.right
            while succ.left:
                succ = succ.left
            return succ

        def find_ancestor_succ(root, p):
            succ = None
            while root != p:
                if p.val < root.val:
                    succ = root
                    root = root.left
                else:
                    root = root.right
            return succ

        return find_descendant_succ(p) if p.right else find_ancestor_succ(root, p)

unreasonably effective