LeetCode 98: Validate Binary Search Tree

Recursive

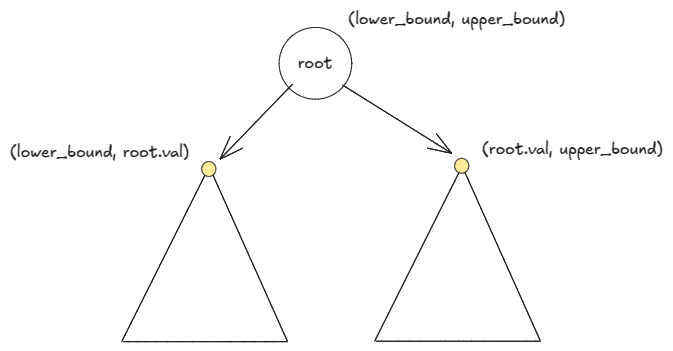
For BST $\forall_{u \in \texttt{left-subtree}} \text{ u}.val < \text{root}.val < \forall_{v \in \texttt{right-subtree}} \text{ v}.val$ . So, for the left subtree, $\text{root}.val$ is an upper bound. Similarly, for the right subtree, $\text{root}.val$ is a lower bound. We recursively validate the invariant: $\text{root}.val \in \left(\texttt{lower-bound}, \texttt{upper-bound}\right)$ .

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(\texttt{tree-height})$ .

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        def is_bst(u, lower_bound, upper_bound):
            if not u:
                return True
            if not (lower_bound < u.val < upper_bound):
                return False
            return is_bst(u.left, lower_bound, u.val) and is_bst(
                u.right, u.val, upper_bound
            )

        return is_bst(root, float("-inf"), float("inf"))

Iterative

With an explicit stack, we simulate the top-down recursion.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        if not root:
            return True
        
        stack = [(root, float("-inf"), float("inf"))]
        while stack:
            u, lower_bound, upper_bound = stack.pop()
            if not (lower_bound < u.val < upper_bound):
                return False
            if u.left:
                stack.append( (u.left, lower_bound, u.val) )
            if u.right:
                stack.append( (u.right, u.val, upper_bound) )

        return True

unreasonably effective