Recursive
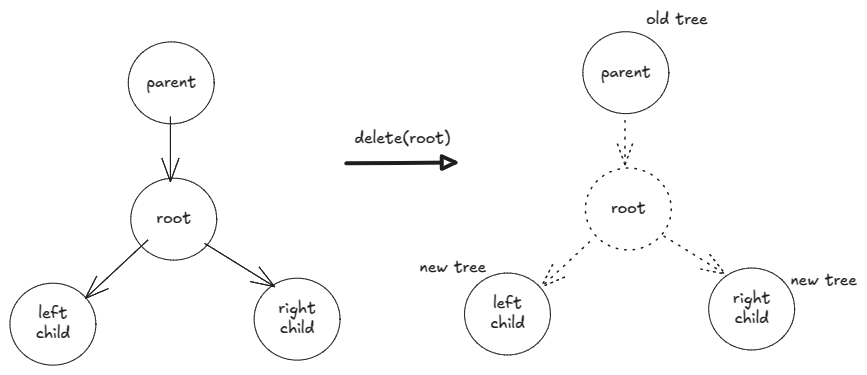
Deleting a node affects at most three other nodes: (1) parent (2) left child (3) right child. After delete, the children become roots of new trees while parent looses one child. So, with a single DFS, for each node, we can update these three pointers while collecting new roots. The updates must be done bottom up, otherwise, we may disconnect a subtree where more deletes needed to happen.
Time: 
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def delete_nodes(self, root, deleted, new_roots) -> Optional[TreeNode]:
if not root:
return None
root.left = self.delete_nodes(root.left, deleted, new_roots)
root.right = self.delete_nodes(root.right, deleted, new_roots)
if root.val not in deleted:
return root
new_roots.extend( c for c in (root.left, root.right) if c )
root.left, root.right = None, None
return None
def delNodes(self, root: Optional[TreeNode], to_delete: List[int]) -> List[TreeNode]:
deleted = set(to_delete)
trees = []
self.delete_nodes(root, deleted, trees)
if root.val not in deleted:
trees.append(root)
return trees
unreasonably effective 
Leave a comment