LeetCode 2458: Height of Binary Tree After Subtree Removal Queries

Recursive

We can simulate deleting of the subtree by considering root.val == q as if it were root.val == None.

Time: $\mathcal{O}(m \cdot n)$ , space: $\mathcal{O}(\texttt{tree-height} + m)$ .

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def height_without_q(self, root, q) -> int:
        if not root or root.val == q:
            return -1

        return (
            max(
                self.height_without_q(root.left, q),
                self.height_without_q(root.right, q),
            )
            + 1
        )

    def treeQueries(self, root: Optional[TreeNode], queries: List[int]) -> List[int]:
        return [self.height_without_q(root, q) for q in queries]

Deleting a rooted subtree may or may not affect the longest simple path.

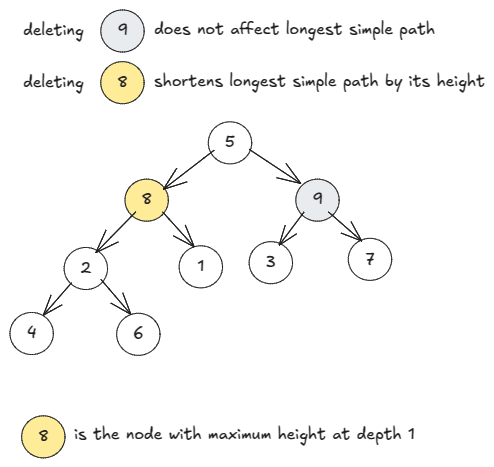
From the level-wise view of the tree we make the below observations:

The longest simple path goes through one node at each depth.
The node at a depth that the path goes through has the the greatest height at that depth.

Given a to-be-deleted node $u$ , we can check if it is the node with the greatest height at its depth. This gives us an efficient way to determine if deleting $u$ will affect the longest simple path.

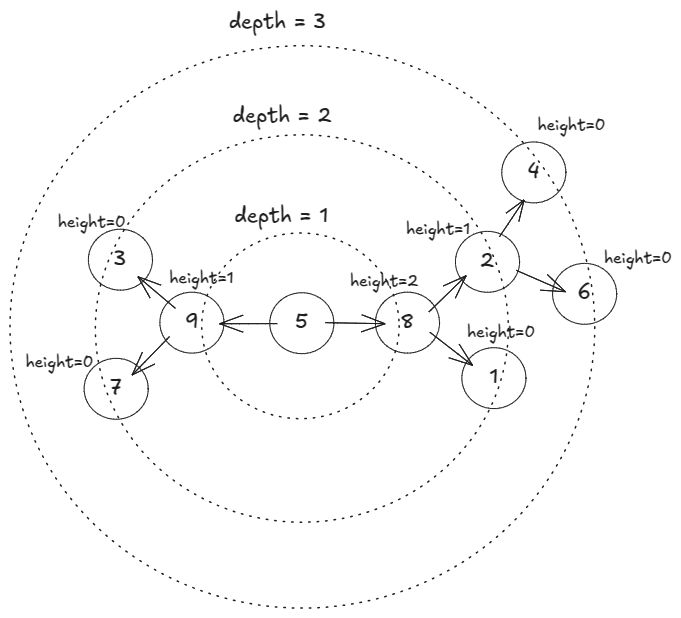
Say, we want to delete the subtree rooted at the node $u$ . Say, its depth is $d_u$ and its height is $h_u$ . Deleting $u$ affects the longest simple path in the below two cases:

is the only node at depth .
- The path stops at the depth $(d_u - 1)$ .
has the greatest height at depth .
- The path goes through the node with the second greatest height at depth $d_u$ .

If we know three pieces of information: (1) each node’s depth, (2) each node’s height, and (3) at each depth the two nodes with max and second max height, then we can efficiently find what the length of the longest path would be if we deleted a rooted subtree. These information can be collected with a single DFS.

Time: $\mathcal{O}(n + |to\_delete|)$ , space: $\mathcal{O}(n)$ .

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def dfs(self, root, depth, coord, level_max) -> int:
        if not root:
            return -1

        left_height = self.dfs(root.left, depth+1, coord, level_max)
        right_height = self.dfs(root.right, depth+1, coord, level_max)
        height = max(left_height, right_height)+1
        coord[root.val] = (depth, height)

        # Keep nodes with max and second max height per depth
        level_max[depth] = level_max.get(depth, []) + [root.val]
        if len(level_max[depth]) > 1:
            level_max[depth].sort(key=lambda x: coord[x][1])
        if len(level_max[depth]) > 2:
            level_max[depth] = level_max[depth][-2:]

        return height

    def treeQueries(self, root: Optional[TreeNode], queries: List[int]) -> List[int]:
        coord, level_max = {}, {}
        self.dfs(root, 0, coord, level_max)
        ans = [-1] * len(queries)
        for i, q in enumerate(queries):
            q_depth, q_height = coord[q]
            if len(level_max[q_depth]) == 1:
                ans[i] = max(0, q_depth-1)
            else:
                ans[i] = q_depth
                second_max, first_max = level_max[q_depth]
                ans[i] += (coord[second_max][1]) if q == first_max else (coord[first_max][1])
        return ans

unreasonably effective