Iterative
For the tree to be symmetric, each level (including missing children) must be a palindrome. With a single BFS we process an entire level per iteration and check if the level is a palindrome.
Time: , space:
.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def is_palindrome(self, q):
i, j = 0, len(q)-1
while i < j:
if (q[i] is None) != (q[j] is None):
return False
if q[i] and q[i].val != q[j].val:
return False
i += 1
j -= 1
return True
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
q = deque([root])
while q:
if not self.is_palindrome(q):
return False
level_len = len(q)
for _ in range(level_len):
u = q.popleft()
if not u:
continue
q.extend(c for c in (u.left, u.right))
return True
Recursive
For a subtree rooted at a node, although we cannot define symmetry in terms of only root and its two children, we can define symmetry in terms of root, children and grand children.
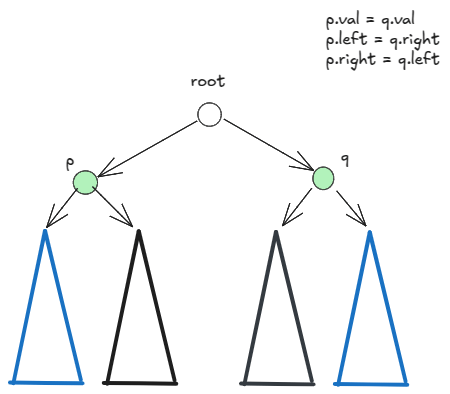
Time: , space:
.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def is_match(self, p, q) -> bool:
if p is None and q is None:
return True
if (p is None) != (q is None):
return False
if p.val != q.val:
return False
return self.is_match(p.left, q.right) and self.is_match(p.right, q.left)
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
return self.is_match(root.left, root.right)
Leave a comment