LeetCode 127: Word Ladder

Unidirectional BFS

The problem is to find the shortest path in an undirected word graph from beginWord to endWord. An edge $(u \leftrightharpoons v)$ means: $v$ is a word in wordList and Hamming distance between the words $u$ and $v$ is 1.

We use BFS. Say $V$ and $E$ are the vertex and edge sets of the word graph. Here, $|V| = | \texttt{wordList} |$ . If word length is $k$ , producing adjacency list of a vertex takes time $k \cdot |\texttt{wordList}|$ .

Time: $\mathcal{O}( k \cdot |\texttt{wordList}|^2 )$ , space: $|\texttt{wordList}|$ .

class Solution:
    def adj_list(self, u: str, word_set: Set[str]) -> Set[str]:
        neibors = set()
        for w in word_set:
            hamming_dist = sum(1 if x != y else 0 for x, y in zip(u, w))
            if hamming_dist != 1:
                continue
            neibors.add(w)

        return neibors

    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
        word_set = set( wordList )

        level = 0
        visited = {beginWord}
        q = deque([beginWord])
        while q:
            level_len = len(q)
            for _ in range(level_len):
                u = q.popleft()

                if u == endWord:
                    return level+1

                for v in self.adj_list(u, word_set):
                    if v in visited:
                        continue
                    visited.add(v)
                    q.append(v)

            level += 1

        return 0

Since alphabet size is 26, for a vertex we could produce all words with Hamming distance = 1 and check if it is in $\texttt{wordList}$ . The cost of producing adjacency list of a vertex is then $\mathcal{O}(k^2)$ — including copy.

Time: $\mathcal{O}(k^2 \cdot |\texttt{wordList}|)$ , space: $\mathcal{O}(|\texttt{wordList}|)$ .

class Solution:
    def adj_list(self, u: str, word_set: Set[str]) -> Set[str]:
        neibors = set()
        u_copy = list(u)
        for i, u_c in enumerate(u):
            for c in ( chr( ord("a")+j ) for j in range(26) ):
                if c == u_c:
                    continue
                u_copy[i] = c
                nei = "".join(u_copy)
                if nei in word_set:
                    neibors.add(nei)
                u_copy[i] = u_c
                
        return neibors

    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
        word_set = set( wordList )

        level = 0
        visited = {beginWord}
        q = deque([beginWord])
        while q:
            level_len = len(q)
            for _ in range(level_len):
                u = q.popleft()

                if u == endWord:
                    return level+1

                for v in self.adj_list(u, word_set):
                    if v in visited:
                        continue
                    visited.add(v)
                    q.append(v)

            level += 1

        return 0

Bi-directional BFS

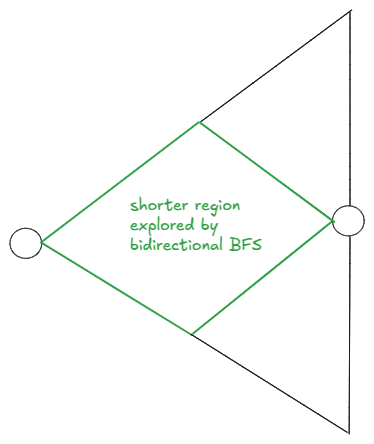
We can do two BFSes at the same time: (1) from beginWord (2) from endWord. At any iteration, if the wavefronts of the two BFSes have a common word say $w$ , we know the shortest path is: $(\texttt{beginWord} \rightarrow w) + (w \rightarrow \texttt{endWord})$ . We end up exploring a shorter region.

from typing import List, Set

class Solution:
    def adj_list(self, u: str, word_set: Set[str]) -> Set[str]:
        neibors = set()
        u_copy = list(u)
        for i, u_c in enumerate(u):
            for c in (chr(ord("a") + j) for j in range(26)):
                if c == u_c:
                    continue
                u_copy[i] = c
                nei = "".join(u_copy)
                if nei in word_set:
                    neibors.add(nei)
                u_copy[i] = u_c
        return neibors

    def bfs(self, source, words) -> Set[str]:
        # We remove a word after it has been visited.
        # So, word_set implicitly tracks visited words.
        word_set = set(words)
        wavefront = {source}
        word_set.discard(source)
        
        while wavefront:
            next_front = set()
            for u in wavefront:
                for v in self.adj_list(u, word_set):
                    next_front.add(v)
                    word_set.remove(v)

            wavefront = next_front
            yield wavefront

    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
        if endWord not in wordList:
            # Even if endWord isn't in the wordList
            # the back BFS will start with endWord
            # and may falsely declare a path.
            return 0
            
        step = 1
        front, back = {beginWord}, {endWord}
        for new_front, new_back in zip( self.bfs(beginWord, wordList), self.bfs(endWord, wordList) ):
            if new_front & back:
                return step+1
            if front & new_back:
                return step+1
            if new_front & new_back:
                return step+2
            front, back = new_front, new_back
            step += 2

        return 0

With zip(), we are producing two new wavefronts at each iteration. Along with the older back and front, we thus end up keeping four wavefronts per iteration. Instead, we can advance only the smaller of the two wavefronts at each iteration. That way:

We shall keep only two wavefronts per iteration
Growth of wavefront remains low.

from typing import List, Set

class Solution:
    def adj_list(self, u: str, word_set: Set[str]) -> Set[str]:
        neibors = set()
        u_copy = list(u)
        for i, u_c in enumerate(u):
            for c in (chr(ord("a") + j) for j in range(26)):
                if c == u_c:
                    continue
                u_copy[i] = c
                nei = "".join(u_copy)
                if nei in word_set:
                    neibors.add(nei)
                u_copy[i] = u_c
        return neibors

    def bfs(self, source, words) -> Set[str]:
        # We remove a word after it has been visited.
        # So, word_set implicitly tracks visited words.
        word_set = set(words)
        wavefront = {source}
        word_set.discard(source)
        
        while wavefront:
            next_front = set()
            for u in wavefront:
                for v in self.adj_list(u, word_set):
                    next_front.add(v)
                    word_set.remove(v)

            wavefront = next_front
            yield wavefront

    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
        if endWord not in wordList:
            # Even if endWord isn't in the wordList
            # the back BFS will start with endWord
            # and may falsely declare a path.
            return 0
            
        step = 1
        front, back = {beginWord}, {endWord}
        front_bfs, back_bfs = self.bfs(beginWord, wordList), self.bfs(endWord, wordList)
        while front:
            if len(front) > len(back):
                front, back = back, front
                front_bfs, back_bfs = back_bfs, front_bfs
            
            front = next(front_bfs)
            if front & back:
                return step+1

            step += 1

        return 0

unreasonably effective