LeetCode 386: Lexicographical Numbers

String sort

Since there are $\lg{n}$ digits in a number, time: $\mathcal{O}(n \cdot \lg{n})$ , space: $\mathcal{O}(n \cdot \lg{n})$ .

class Solution:
    def lexicalOrder(self, n: int) -> List[int]:
        nums = [str(x) for x in range(1, n+1)]
        nums.sort()
        return [int(x_str) for x_str in nums]

DFS in a Trie

There are $\lg{n}$ digits in a number. So, building the trie and a DFS of the trie, both take time $\mathcal{O}(n \cdot \lg{n})$ .

Time: $\mathcal{O}(n \cdot \lg{n})$ , space: $\mathcal{O}(n \cdot \lg{n})$ .

class TrieNode:
    def __init__(self):
        self.end_of_word = False
        # For digits: 0, 1, 2, ..., 9
        self.edges = [None for _ in range(10)]

class Trie:
    def __init__(self):
        self.root = TrieNode()
    
    def insert(self, num_str):
        u = self.root
        for char in num_str:
            digit = int(char)
            if not u.edges[digit]:
                u.edges[digit] = TrieNode()
            u = u.edges[digit]
        u.end_of_word = True
    
    def __collect(self, u, curr_num, nums):
        if u.end_of_word:
            nums.append( int( "".join(curr_num) ) )
        
        for digit in range(10):
            v = u.edges[digit]
            if not v:
                continue
            curr_num.append(str(digit))
            self.__collect(v, curr_num, nums)
            curr_num.pop()


    def numbers(self):
        nums = []
        self.__collect(self.root, [], nums)
        return nums

class Solution:
    def lexicalOrder(self, n: int) -> List[int]:
        trie = Trie()
        for x in range(1, n+1):
            trie.insert(str(x))
        
        return trie.numbers()

DFS in implicit Trie

We could traverse the trie without explicitly building it.

We produce and visit each number once and as an integer. So, time: $\mathcal{O}(n)$ , extra space is the depth of DFS or the digit count: $\mathcal{O}(\lg{n})$ .

class Solution:
    def dfs(self, x, numbers, limit):
        if x > limit:
            return
         
        numbers.append(x)
        for digit in range(10):
            y = 10*x + digit
            self.dfs(y, numbers, limit)
 
    def lexicalOrder(self, n: int) -> List[int]:
        sorted_numbers = []
        for digit in range(1, 10):
            if len(sorted_numbers) == n:
                break
            self.dfs(digit, sorted_numbers, n)
         
        return sorted_numbers

Iterative DFS

Without limit, the DFS explores a forest of nine infinite trees with roots $1, 2, \ldots, 9$ . With $n$ as the limit, the DFS explores only a part of these trees. Exploring first $n$ nodes, within limit, gives us the numbers, $[1, 2, \ldots, n]$ , in sorted order.

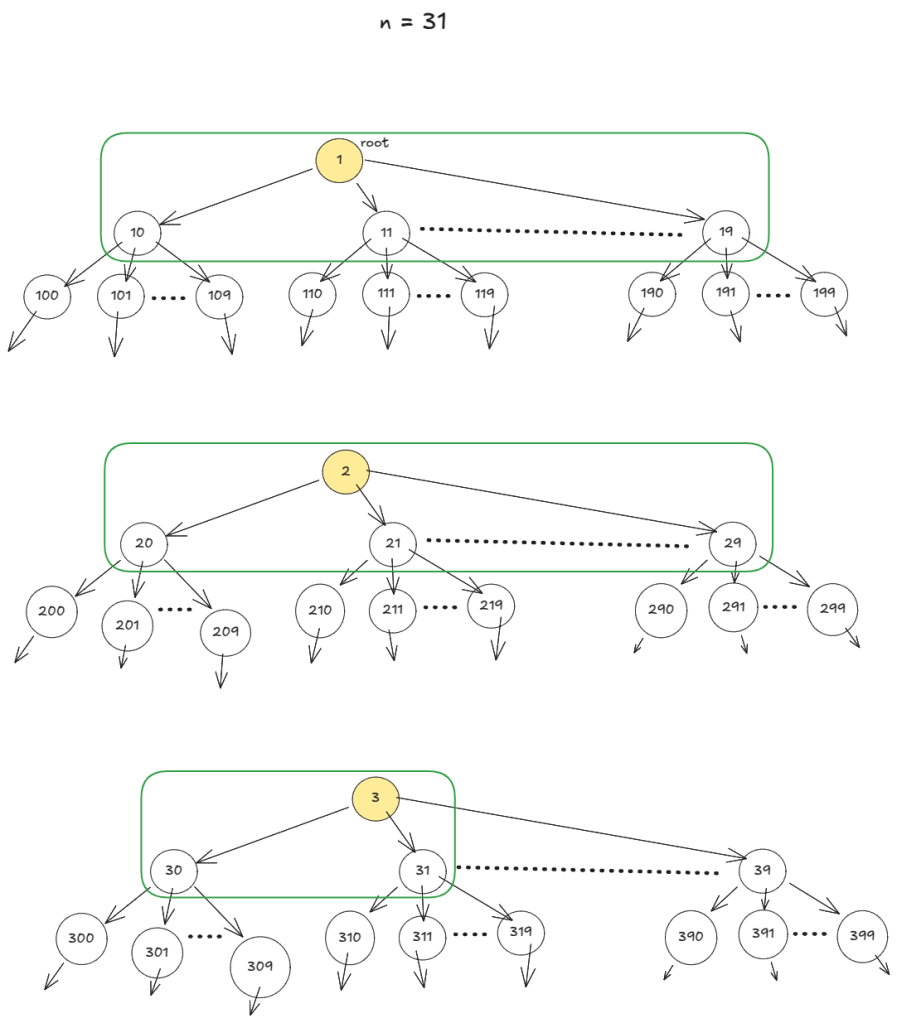
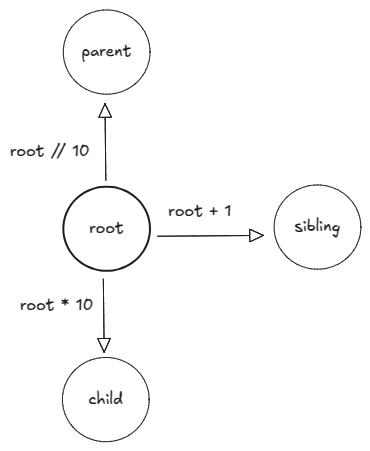
For a node, child, parent and sibling can be found with arithmetic operations. So, iterative DFS of the the implicit tree does not require a stack. Last node on a level has $9$ in its one’s place.

We visit $n$ nodes and each node is visited at most twice. Time: $\mathcal{O}(n)$ , extra space: $\mathcal{O}(1)$ .

class Solution:
    def lexicalOrder(self, n: int) -> List[int]:
        is_last_child = lambda root: root % 10 == 9
        child = lambda root: root * 10
        parent = lambda root: root // 10
        sibling = lambda root: root + 1
 
        sorted_numbers = []
        root = 1
        while len(sorted_numbers) < n:
            sorted_numbers.append(root)
 
            if child(root) <= n:
                root = child(root)
                continue
             
            # Backtrack
            while is_last_child(root) or root == n:
                # If root == n, we have already included it
                root = parent(root)
             
            root = sibling(root)
         
        return sorted_numbers

unreasonably effective