unreasonably effective

link

Try all substrings

For a substring with end-points: (begin, end), length of the set() of characters is the appeal.

Time: , space: .

class Solution:
    def appealSum(self, s: str) -> int:
        n = len(s)
        appeal = 0
        for begin in range(n):
            chars = set()
            for end in range(begin, n):
                chars.add(s[end])
                appeal += len(chars)

        return appeal

Prefix appeals

Above, we are already quite efficient, taking only time per substring. So, if we want to be more efficient, say take total time, we cannot iterate over all substrings. For each index we must find total appeal up to that index in time.

Observations:

1. There are (i+1) substrings that end at s[i].
2. Appeal of a substring is at least 1 and at most len(substring).
3. For a substring, it does not matter if we compute appeal left-to-right or right-to-left.

Say is the total appeal of the prefix s[0 : i+1], then it is related to in the below way:

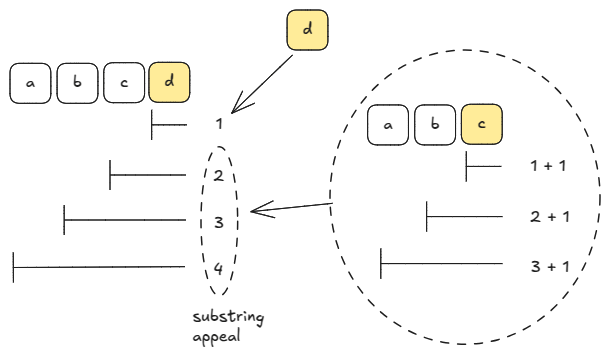
Above, since "d" does not appear in the prefix "abc", it adds 1 to all previous substring-appeals. So, Appeal("abcd") = Appeal("abc") + len("abc") + 1, where the 1 comes from the one-length substring "d".

On the other hand, if "d" appears in the earlier prefix, it increases substring-appeals by 1 up to (but excluding) the index where we last saw "d":

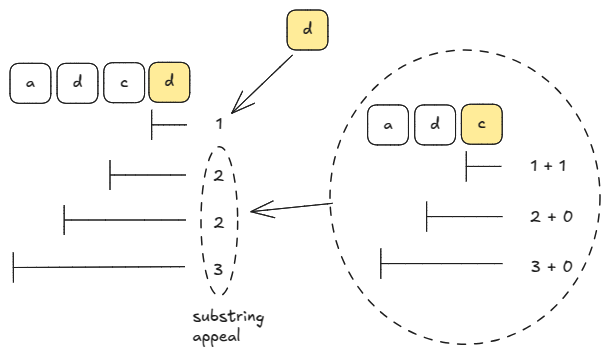
So, if we keep track of two pieces of information: (1) which index we last saw a character (2) appeal of previous prefix, we can compute the total appeal of all substrings that end at an index in time.

Time: , space: .

class Solution:
    def appealSum(self, s: str) -> int:
        prev_appeal = 0
        total_appeal = 0
        last_seen_at = {}
        for i, c in enumerate(s):
            pos = last_seen_at.get(c, -1)
            curr_appeal = prev_appeal + (i-pos)
            total_appeal += curr_appeal
            
            last_seen_at[c] = i
            prev_appeal = curr_appeal

        return total_appeal