unreasonably effective

Say we have an equivalence relation on a set . So, partitions into equivalence classes which are disjoint subsets of . Now, given a pair where , we want to answer: Do and belong to the same equivalence class?

As an example, we need to answer this question to build the minimum spanning tree of an weighted, undirected graph like below.

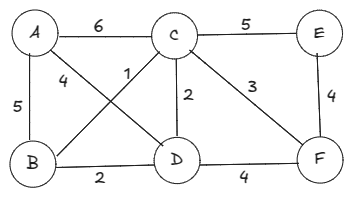
Here, the vertex set is and the equivalence relation = . Therefore, = From to there is a path.

We start with equivalence classes or connected-components and we end up with a single connected component. In the process, we consider edges in non-decreasing order of their weights (lightest to heaviest). We add the edge to the spanning tree only if do not belong to the same equivalence class or connected-component — ensuring every added edge reduces the number of connected-components by one.

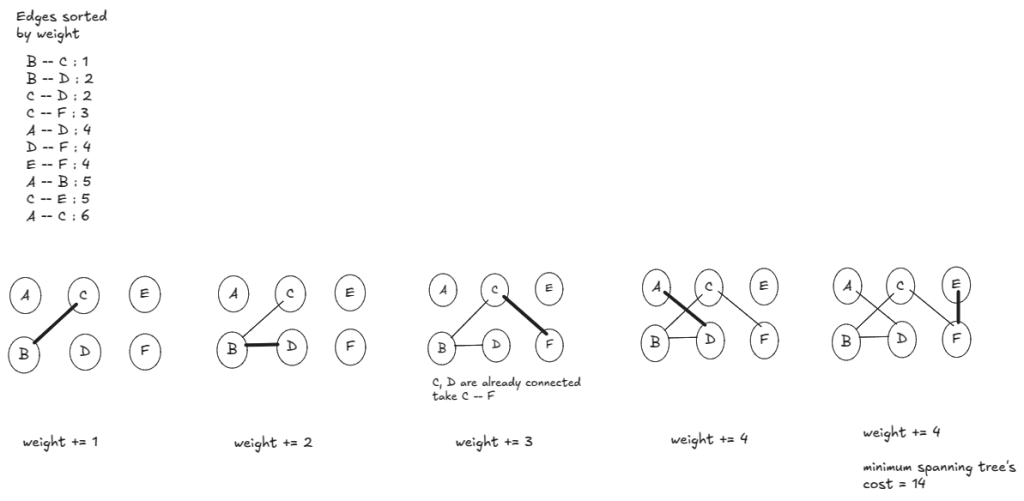
Union-find is a data structure that lets us answer this question efficiently using tree-representation for each equivalence class or partition.

class UnionFind:
    def __init__(self, S):
        self.parent_of = {a: a for a in S}
        self.rank_of = {a: 0 for a in S}

    def find(self, a):
        root = a
        while root != (p := self.parent_of[root]):
            root = p
        return root

    def union(self, a, b):
        root_a = self.find(a)
        root_b = self.find(b)
        if root_a == root_b:
            return

        rank_a = self.rank_of[root_a]
        rank_b = self.rank_of[root_b]
        if rank_a == rank_b:
            self.parent_of[root_a] = root_b
            self.rank_of[root_b] += 1
            return

        if rank_a < rank_b:
            self.parent_of[root_a] = root_b
        else:
            self.parent_of[root_b] = root_a

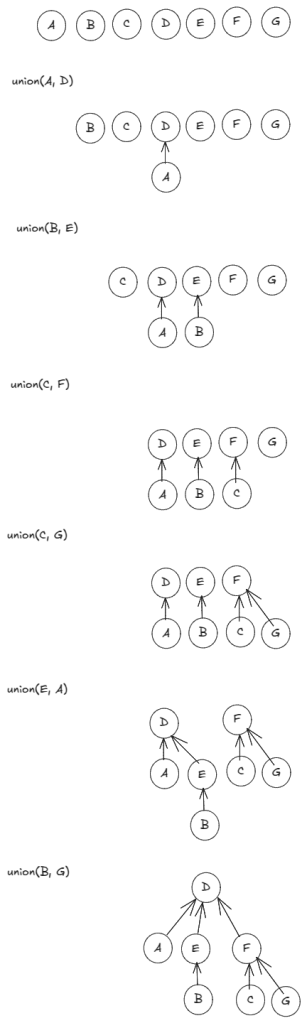
For the minimum spanning tree, for an edge (a, b) if find(a) == find(b), the two vertices a and b are already connected, so we would not include the edge (a, b) in the spanning tree. If, on the other hand, find(a) != find(b), we would include the edge in the spanning tree and by union(a, b) would put a and b in the same connected component.

Note, rank_a is the height of the root of the tree that contains a. And, both find() and union() take time .

If , the maximum rank is .

Because, a root of rank is created from merging two roots of rank . So, the count of nodes in a subtree has the recurrence relation: . As a consequence, there are at most roots with height — implying the maximum value of is .

Operation	Time	Space
__init__
find
union

Path compression

During find(), we can compress the path from the node a to its root — making subsequent find()‘s faster.

class UnionFindPC:
    def __init__(self, S):
        self.parent_of = {a: a for a in S}
        self.rank_of = {a: 0 for a in S}

    def __compress_path(self, a, root):
        while a != (p := self.parent_of[a]):
            self.parent_of[a] = root
            a = p
    
    def find(self, a):
        root = a
        while root != self.parent_of[root]:
            root = self.parent_of[root]
        self.__compress_path(a, root)
        return root

    def union(self, a, b):
        root_a = self.find(a)
        root_b = self.find(b)
        if root_a == root_b:
            return

        rank_a = self.rank_of[root_a]
        rank_b = self.rank_of[root_b]
        if rank_a == rank_b:
            self.parent_of[root_a] = root_b
            self.rank_of[root_b] += 1
            return

        if rank_a < rank_b:
            self.parent_of[root_a] = root_b
        else:
            self.parent_of[root_b] = root_a