LeetCode 218: The Skyline Problem

For skyline, building roofs are important.

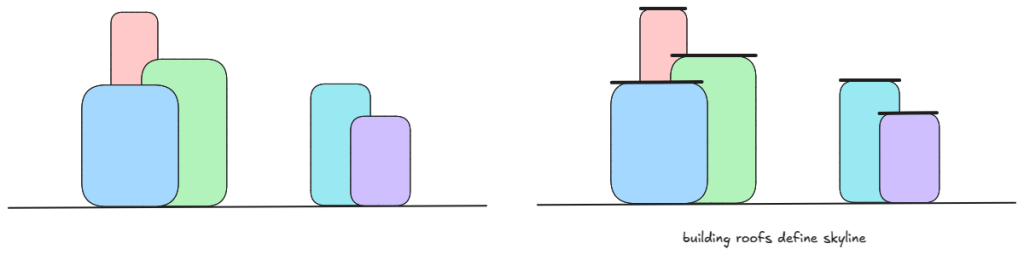
Roofs are intervals at some height.

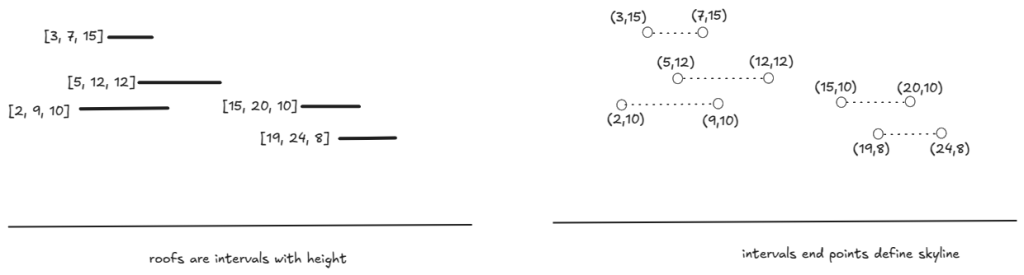
If we jump from the end of a roof, we fall to the next higher roof or we fall to the ground.

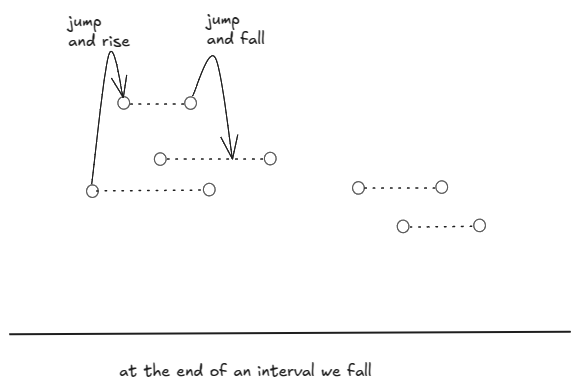
We can find the skyline points from the groups of heights at different locations — from each group, just take the point at the maximum height.

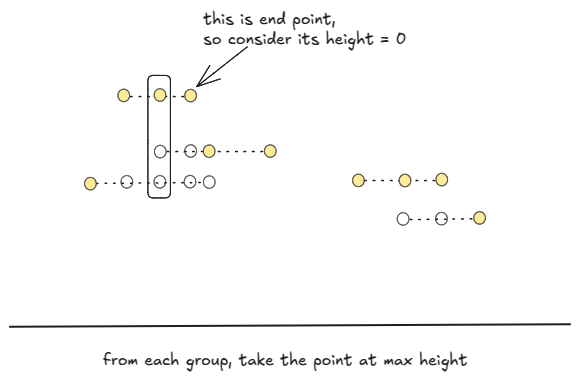
In the end, we can merge consecutive points at the same height.

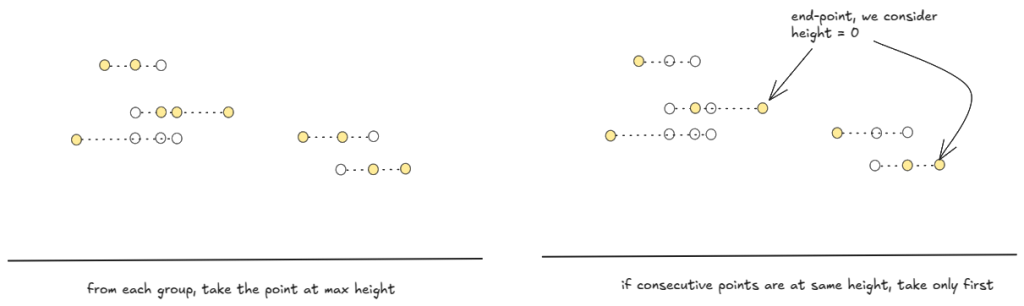
Linear scan and groups

For each building-endpoint, to find co-located heights, we do linear scan.

If there are $n$ buildings, time: $\mathcal{O}(n^2 + n \cdot \lg{n})$ , space: $\mathcal{O}(n^2)$ .

class Solution:
    def get_colocated_heights(self, loc, buildings):
        heights = set()
        for a, b, h in buildings:
            if loc < a or loc > b:
                continue
            heights.add( 0 if loc == b else h )
        return heights

    def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
        colocated_heights = {}
        for a, b, h in buildings:
            if a not in colocated_heights:
                colocated_heights[a] = set()
            colocated_heights[a].add( h )
            colocated_heights[a].update( self.get_colocated_heights(a, buildings) )

            if b not in colocated_heights:
                colocated_heights[b] = set()
            colocated_heights[b].add( 0 )
            colocated_heights[b].update( self.get_colocated_heights(b, buildings) )

        skyline = []
        for loc in sorted(colocated_heights):
            h = max( colocated_heights[loc] )
            if skyline and skyline[-1][1] == h:
                continue
            skyline.append([loc, h])

        return skyline

Linear scan and group max

For a location, we only need the maximum height.

Time: $\mathcal{O}(n^2)$ , space: $\mathcal{O}(n)$ .

class Solution:
    def get_max_height_at(self, loc, buildings):
        max_height = 0
        for a, b, h in buildings:
            if loc < a or loc > b:
                continue
            max_height = max(max_height, 0 if loc == b else h)
        return max_height

    def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
        max_height_at = {}
        for a, b, h in buildings:
            max_height_at[a] = self.get_max_height_at(a, buildings)
            max_height_at[b] = self.get_max_height_at(b, buildings)

        skyline = []
        for loc in sorted(max_height_at):
            h = max_height_at[loc]
            if skyline and skyline[-1][1] == h:
                continue
            skyline.append([loc, h])

        return skyline

List of all possible points

If we have a list of points [0, max(roof-ends)], for a roof [a, b, h] we can update the heights of all b-a+1 points in that list.

Say max(roof-ends) = $\epsilon$ and max(roof-width) = $w$ .

Time: $\mathcal{O}(\epsilon \cdot w)$ , space: $\mathcal{O}(\epsilon)$ .

class Solution:
    def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
        right_most_loc = max( end for _, end, _ in buildings )
        max_height_at = [float("-inf") for _ in range(right_most_loc+1)]
        for a, b, h in buildings:
            for loc in range(a, b):
                max_height_at[loc] = max( max_height_at[loc], h )
            max_height_at[b] = max( max_height_at[b], 0 )

        skyline = []
        for loc, h in enumerate(max_height_at):
            if h == float("-inf"):
                continue
            if skyline and skyline[-1][1] == h:
                continue
            skyline.append([loc, h])

        return skyline

Linear scan through roof end-points

We only need to update the roof endpoint locations. So, for a roof [left, right], instead of updating all points, we can update only existent roof endpoints in [left, right].

Time: $\mathcal{O}(n^2)$ , space: $\mathcal{O}(n)$ .

class Solution:
    def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
        max_height_at = {}
        for left, right, h in buildings:
            if left not in max_height_at:
                max_height_at[left] = h
            else:
                max_height_at[left] = max( max_height_at[left], h )
            
            if right not in max_height_at:
                max_height_at[right] = 0
        
        for left, right, h in buildings:
            for loc in max_height_at:
                if loc < left or loc >= right:
                    continue
                max_height_at[loc] = max( max_height_at[loc], h )
        
        skyline = []
        for loc in sorted(max_height_at):
            h = max_height_at[loc]
            if skyline and skyline[-1][1] == h:
                continue
            skyline.append( [loc, h] )
        
        return skyline

Binary search in roof-endpoints

Instead of linear scan, we could binary-search the roof end points.

Time: $\mathcal{O}(n \cdot \lg{n} + n \cdot w)$ , space: $\mathcal{O}(n)$ .

class Solution:
    def find_location(self, x, locations):
        lo, hi = 0, len(locations)-1
        while lo <= hi:
            mid = (lo + hi) // 2
            if x == locations[mid]:
                return mid
            
            if locations[mid] < x:
                lo = mid+1
            else:
                hi = mid-1

        return -1

    def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
        max_height_at = {}
        for left, right, h in buildings:
            if left not in max_height_at:
                max_height_at[left] = h
            else:
                max_height_at[left] = max( max_height_at[left], h )
            
            if right not in max_height_at:
                max_height_at[right] = 0
        
        locations = sorted(x for x in max_height_at)
        for left, right, h in buildings:
            left_pos = self.find_location(left, locations)
            right_pos = self.find_location(right, locations)
            for i in range(left_pos, right_pos):
                loc = locations[i]
                max_height_at[loc] = max( max_height_at[loc], h )
        
        skyline = []
        for loc in locations:
            h = max_height_at[loc]
            if skyline and skyline[-1][1] == h:
                continue
            skyline.append( [loc, h] )
        
        return skyline

unreasonably effective