All equations and valid queries are divisions. So, we can we can model a valid query, as a weighted path between
and
.
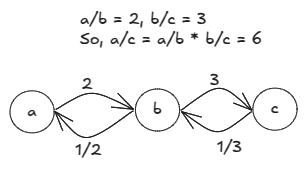
We build a graph of variables where the edge has weight
. We also get the edge
with weight
. As we build the adjacency list of the graph, we also build Union-Find, which helps detect invalid queries in essentially
time. To evaluate
, we back-track to find the path from
to
.
Say there are variables and
equations.
| Operation | Time | Space |
| Build adjacency list | ||
| Build Union-Find | ||
| Valid query | ||
| Invalid query |
class UnionFind:
def __init__(self):
self.parent_of = {}
self.rank_of = {}
def __compress_path(self, u, root):
while u != (p := self.parent_of[u]):
self.parent_of[u] = root
u = p
def __find(self, u):
root = u
while root != (p := self.parent_of[root]):
root = p
self.__compress_path(u, root)
return root
def add_vertex(self, u):
self.parent_of[u] = u
self.rank_of[u] = 0
def union(self, u, v):
root_u = self.__find(u)
root_v = self.__find(v)
if root_u == root_v:
return
rank_u = self.rank_of[u]
rank_v = self.rank_of[v]
if rank_u == rank_v:
self.parent_of[root_u] = root_v
self.rank_of[root_v] += 1
return
if rank_u < rank_v:
self.parent_of[root_u] = root_v
else:
self.parent_of[root_v] = root_u
def is_connected(self, u, v):
root_u = self.__find(u)
root_v = self.__find(v)
return root_u == root_v
class Solution:
def evaluate(self, a, c, adj_list, visited):
if a == c:
return 1.0
visited.add(a)
for b, val in adj_list[a]:
if b in visited:
continue
result = self.evaluate(b, c, adj_list, visited)
if result is not None:
return val * result
visited.remove(a)
def calcEquation(
self, equations: List[List[str]], values: List[float], queries: List[List[str]]
) -> List[float]:
uf = UnionFind()
adj_list = {}
for pair, val in zip(equations, values):
u, v = pair
if u not in adj_list:
adj_list[u] = []
uf.add_vertex(u)
if v not in adj_list:
adj_list[v] = []
uf.add_vertex(v)
adj_list[u].append((v, val))
adj_list[v].append((u, 1 / val))
uf.union(u, v)
ans = []
for a, c in queries:
if a not in adj_list or c not in adj_list:
ans.append(-1.0)
continue
if not uf.is_connected(a, c):
ans.append(-1.0)
continue
ans.append(self.evaluate(a, c, adj_list, set()))
return ans
Leave a comment