LeetCode 716: Max Stack

Stack of (num, curr_max)

We can keep current max with the element.

Say len(stack) = $n$ .

class MaxStack:

    def __init__(self):
        self.stack = []

    def push(self, x: int) -> None:
        if not self.stack:
            self.stack.append( [x, x] )
            return
        
        _, top_max = self.stack[-1]
        curr_max = max(top_max, x)
        self.stack.append( [x, curr_max] )

    def pop(self) -> int:
        x, _ = self.stack.pop()
        return x

    def top(self) -> int:
        x, _ = self.stack[-1]
        return x

    def peekMax(self) -> int:
        _, top_max = self.stack[-1]
        return top_max

    def popMax(self) -> int:
        _, curr_max = self.stack[-1]
        peeks = []
        while self.stack and self.stack[-1][0] != self.stack[-1][1]:
            peeks.append( self.stack[-1][0] )
            self.stack.pop()
        self.stack.pop()

        while peeks:
            self.push(peeks.pop())

        return curr_max

# Your MaxStack object will be instantiated and called as such:
# obj = MaxStack()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.top()
# param_4 = obj.peekMax()
# param_5 = obj.popMax()

Above, in the worst-case, popMax() needs to sift through the entire stack. To make finding max faster, we can use max heap.

LinkedList and Max-Heap

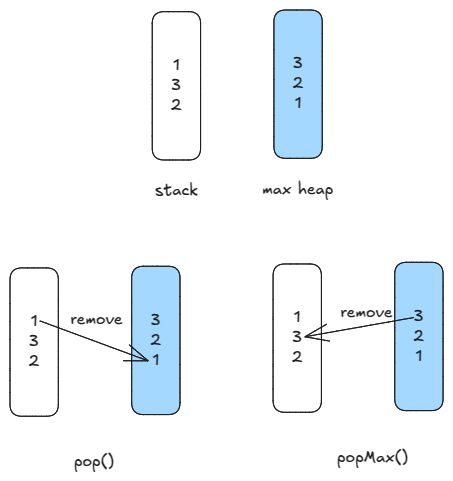
We keep two stacks: one for values and one for maxes. For maxes, we use a max heap with the value as the primary key and an increasing id as the secondary key.

On popMax(), we need to remove the latest max from the value stack as well. The latest max may appear in the middle of the value stack and deleting it creates a hole. So, we use a LinkedList as the value stack. Similarly, when we pop(), we need to remove the top from the max heap. Since, max-heap does not support efficient delete, we just mark the item as deleted. When we do peekMax() or popMax() again, we get rid of the tops which are marked as deleted.

popMax or peekMax has amortized time $\mathcal{O}(\lg{n})$ . Say we made $n$ pushes. Now, we did $(n-1)$ pops. We do a popMax. It can trigger $n$ pops from the max heap which has total cost $n \cdot \lg{n}$ , so per push the cost is amortized to $\lg{n}$ .

from heapq import heappush as push, heappop as pop

class ListNode:
    def __init__(self, val):
        self.val = val
        self.prev, self.next = None, None

class LinkedList:
    def __init__(self):
        self.head, self.tail = None, None
    
    def append(self, node):
        if not self.tail:
            self.tail = node
            self.head = node
            return

        self.tail.next = node
        node.prev = self.tail
        self.tail = self.tail.next

    def top(self):
        return self.tail
    
    def pop(self):
        node = self.tail
        if not self.tail.prev:
            self.tail = None
            self.head = None
            return node

        self.tail = self.tail.prev
        self.tail.next = None
        return node

    def remove(self, node):
        prev_node, next_node = node.prev, node.next
        if not prev_node:
            # node is head
            self.head = self.head.next
            if self.head:
                self.head.prev = None
            else:
                self.tail = None
            node.prev, node.next = None, None
            return
        
        if not next_node:
            # node is tail
            self.tail = self.tail.prev
            self.tail.next = None
            node.prev, node.next = None, None
            return

        prev_node.next = next_node
        next_node.prev = prev_node
        node.prev, node.next = None, None


class MaxStack:

    def __init__(self):
        self.deleted_nodes = set()
        self.id = -1
        self.stack = LinkedList()
        self.maxq = []

    def push(self, x: int) -> None:
        self.id += 1
        node = ListNode(x)
        self.stack.append(node)
        push( self.maxq, (-x, -self.id, node) )

    def pop(self) -> int:
        node = self.stack.pop()
        self.deleted_nodes.add(node)
        return node.val

    def top(self) -> int:
        top_node = self.stack.top()
        return top_node.val

    def __remove_stale_nodes(self):
        while self.maxq:
            *_, node = self.maxq[0]
            if node not in self.deleted_nodes:
                break
            pop(self.maxq)
            self.deleted_nodes.remove(node)

    def peekMax(self) -> int:
        self.__remove_stale_nodes()
        
        neg_x, *_ = self.maxq[0]
        return -neg_x        

    def popMax(self) -> int:
        self.__remove_stale_nodes()
        
        neg_x, _, node = pop(self.maxq)
        self.stack.remove(node)
        return -neg_x


# Your MaxStack object will be instantiated and called as such:
# obj = MaxStack()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.top()
# param_4 = obj.peekMax()
# param_5 = obj.popMax()

LinkedList and Updatable Max-Heap

Above, if we do not call popMax for a while, the heap operations can get slow.

If our max heap supported updating key in $\mathcal{O}(\lg{n})$ time, instead of marking it deleted, we could update the key to $+\infty$ and then do a pop from the max heap. This ensures, instead of amortized, every popMax has time $\mathcal{O}(\lg{n})$ .

Operation	Time	Space
`__init__`	$\mathcal{O}(1)$	$\mathcal{O}(1)$
`push`	$\mathcal{O}(1)$	$\mathcal{O}(1)$
`pop`	$\mathcal{O}(1)$	$\mathcal{O}(1)$
`top`	$\mathcal{O}(1)$	$\mathcal{O}(1)$
`peekMax`	$\mathcal{O}(1)$	$\mathcal{O}(1)$
`popMax`	$\mathcal{O}(n)$	$\mathcal{O}(n)$

Operation	Time	Space
`__init__`	$\mathcal{O}(1)$	$\mathcal{O}(1)$
`push`	$\mathcal{O}(\lg{n})$	$\mathcal{O}(1)$
`pop`	$\mathcal{O}(1)$	$\mathcal{O}(1)$
`top`	$\mathcal{O}(1)$	$\mathcal{O}(1)$
`peekMax`	$\mathcal{O}(\lg{n})$	$\mathcal{O}(1)$
`popMax`	$\mathcal{O}(\lg{n})$	$\mathcal{O}(1)$

unreasonably effective