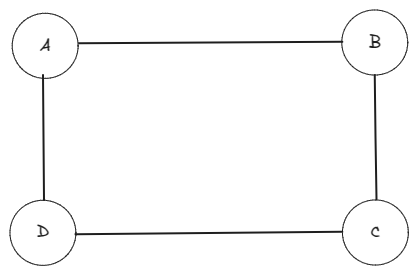
For each pair of points we consider one as top-left (A) and the other as bottom-right (C) corner of an axis-aligned rectangle. Then, we try finding B and D. Once we have found all four corners, we check if other points lie on the rectangle, if not, we include it in max area computation.
Time: 
class Solution:
def contains_other_points(self, A, B, C, D, point_set):
rectangle_corners = {A, B, C, D}
left, right, top, bottom = A[0], B[0], A[1], C[1]
for p in point_set:
if p in rectangle_corners:
continue
x, y = p
if left <= x <= right and bottom <= y <= top:
return True
return False
def maxRectangleArea(self, points: List[List[int]]) -> int:
points.sort()
point_set = set(tuple(p) for p in points)
max_area = float("-inf")
for i in range(len(points)):
for j in range(i + 1, len(points)):
A = tuple(points[i])
C = tuple(points[j])
dx, dy = C[0] - A[0], A[1] - C[1]
if dx <= 0 or dy <= 0:
continue
B, D = (A[0] + dx, A[1]), (A[0], A[1] - dy)
if (B not in point_set) or (D not in point_set):
continue
if self.contains_other_points(
A, B, C, D, point_set
):
continue
max_area = max(max_area, dx * dy)
return max(-1, max_area)
unreasonably effective 
Leave a comment