unreasonably effective

you can be sloppy, as long as you are rigorous

LeetCode 1650: Lowest Common Ancestor of a Binary Tree III

link

Since we have parent pointer, we can find the path from p -> root and q -> root and then traverse the two paths in sync to find the LCA.

Time: \mathcal{O}(\texttt{tree-height}), space: \mathcal{O}(\texttt{tree-height}).

"""
# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None
"""

class Solution:
    def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
        p_path = []
        curr = p
        while curr:
            p_path.append(curr)
            curr = curr.parent
        
        q_path = []
        curr = q
        while curr:
            q_path.append(curr)
            curr = curr.parent
        
        short_path, long_path = (p_path, q_path) if len(p_path) <= len(q_path) else (q_path, p_path)
        i, j = 0, len(long_path)-len(short_path)
        while short_path[i] != long_path[j]:
            i += 1
            j += 1
        
        return short_path[i]

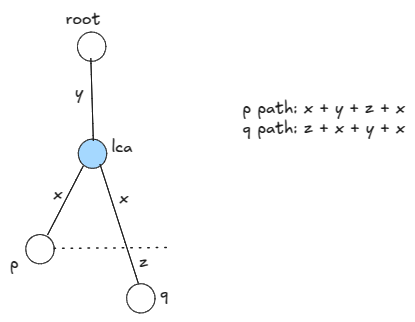
We do not need to precompute the paths. Say p and q are traversing towards the root. Below, by the time p reaches root, q is just z nodes behind. So, if we can make p take a detour of extra z nodes, then p and q will be synced and later they will meet at LCA.

Time: \mathcal{O}(\texttt{tree-height}), space: \mathcal{O}(1).

"""
# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None
"""

class Solution:
    def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
        a, b = p, q
        while a != b:
            a = a.parent or q
            b = b.parent or p
        
        return a

tanvirdotzaman

Leave a comment