LeetCode 727: Minimum Window Subsequence

Starting at each index of s1 we can try matching s2.

Say len(s1) = $n$ and len(s2) = $m$ .

Time: $\mathcal{O}(n^2)$ , space: $\mathcal{O}(1)$ .

class Solution:
    def match_window(self, text, begin, pattern):
        i, j = 0, begin
        while i < len(pattern) and j < len(text):
            if pattern[i] == text[j]:
                i += 1
            j += 1

        return j-1 if i == len(pattern) else None

    def minWindow(self, s1: str, s2: str) -> str:
        min_len = float("inf")
        left, right = None, None
        for i, c in enumerate(s1):
            if c != s2[0]:
                continue
                
            end = self.match_window(s1, i, s2)
            if end is None:
                continue
            
            window_len = end-i+1
            if window_len < min_len:
                min_len = window_len
                left, right = i, end
            
        return "" if left is None else s1[left : right+1]

The window in s1 that contains s2 as a subsequence must have all characters of s2. So, to decrease the number of match_window() calls, we may first try finding the minimum window of s1 that contains all characters in s2 and then match order. Below example shows this would not work.

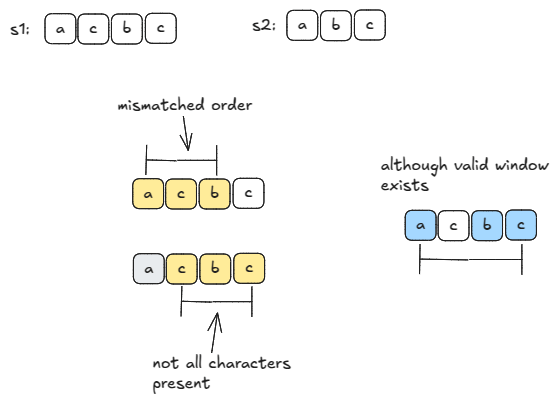
Expand and shrink

We can expand the sliding window until we find all chars of s2 in order. Then we do a backward scan from the end to find the minimum length window. Now, we can shrink the entire window past the min-window’s first char.

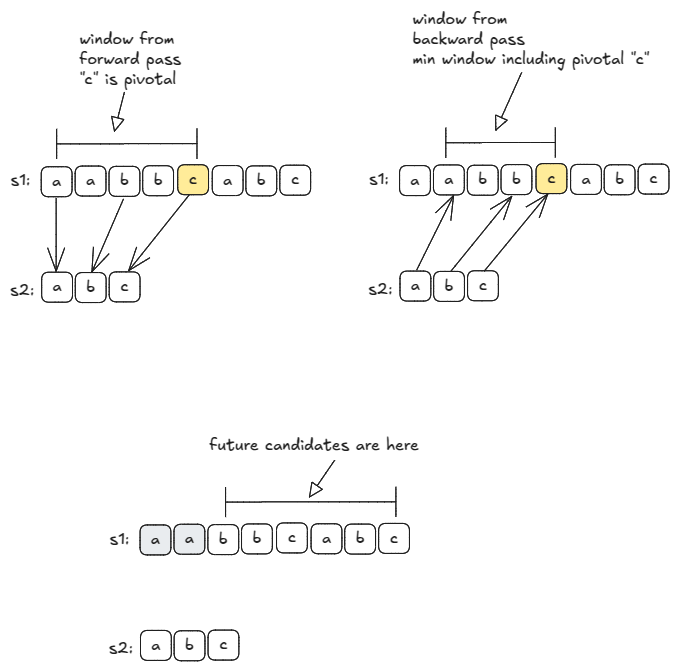
Worst-case time is when each char in s1 triggers a backward pass like the example below:

Time: $\mathcal{O}(n \cdot m)$ , space: $\mathcal{O}(1)$ .

class Solution:
    def minWindow(self, s1: str, s2: str) -> str:
        i, j = 0, 0
        n, m = len(s1), len(s2)
        min_len = float("inf")
        left, right = None, None
        while i < n:
            if s1[i] != s2[j]:
                i += 1
                continue
            
            if j < m-1:
                i += 1
                j += 1
                continue
            
            # last char of s2 has been matched
            end = i
            j = m-1
            while j >= 0:
                if s1[i] == s2[j]:
                    j -= 1
                i -= 1
            begin = i+1
            
            window_len = end-begin+1
            if window_len < min_len:
                min_len = window_len
                left, right = begin, end
            
            i, j = begin+1, 0

        return "" if left is None else s1[left : right+1]

unreasonably effective