LeetCode 759: Employee Free Time

Pre-sort

A single employee’s free times are the gaps between consecutive work intervals.

For more than one employees, we can merge overlapping work intervals and have a list of disjoint work intervals across all employees. Then, free times once again would be the gaps between consecutive work intervals.

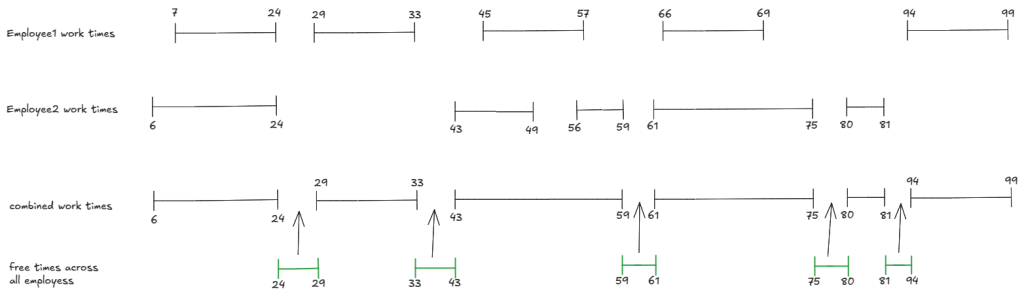
Say there are $n$ employees and the longest employee work time list has length $m$ .

Time: $\mathcal{O}(n \cdot m \cdot \lg{(n \cdot m)})$ , space: $\mathcal{O}(n \cdot m)$ .

"""
# Definition for an Interval.
class Interval:
    def __init__(self, start: int = None, end: int = None):
        self.start = start
        self.end = end
"""


class Solution:
    def merge_intervals(self, intervals):
        merged_intervals = []
        prev = intervals[0]
        for i in range(1, len(intervals)):
            curr = intervals[i]
            if prev.end < curr.start:
                merged_intervals.append(prev)
                prev = curr
            else:
                prev = Interval(prev.start, max(prev.end, curr.end))

        merged_intervals.append(prev)

        return merged_intervals

    def employeeFreeTime(self, schedule: "[[Interval]]") -> "[Interval]":
        all_intervals = sum(schedule, [])
        all_intervals.sort(key=lambda x: x.start)

        intervals = self.merge_intervals(all_intervals)
        free_time_list = []
        for i in range(1, len(intervals)):
            prev = intervals[i - 1]
            curr = intervals[i]
            free_time_list.append(Interval(prev.end, curr.start))

        return free_time_list

MinHeap

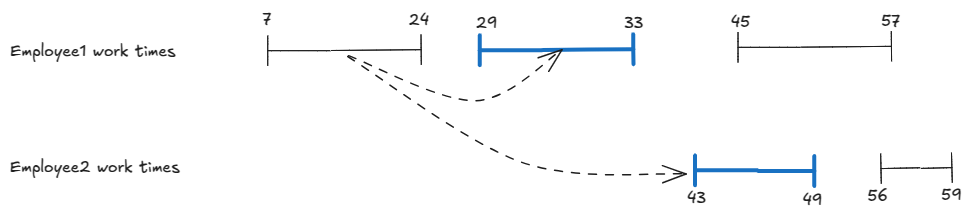
The work time list of an employee is already sorted. With list heads in a min-heap, we can skip the pre-sorting + merging — we can merge and find gap as we go.

In the min-heap, to find the gap between consecutive work intervals, the top work interval must be compared with two work intervals: (1) the second-top and (2) top’s next.

Time: $\mathcal{O}(n \cdot m \cdot \lg{n})$ , space: $\mathcal{O}(n)$ .

from heapq import heapify, heappush as push, heappop as pop

"""
# Definition for an Interval.
class Interval:
    def __init__(self, start: int = None, end: int = None):
        self.start = start
        self.end = end
"""


class EmployeeWork:
    def __init__(self, times, index):
        self.times = times
        self.index = index

    def start(self):
        return self.times[self.index].start

    def end(self):
        return self.times[self.index].end

    def has_next(self):
        return self.index < len(self.times) - 1

    def next(self):
        return EmployeeWork(
            self.times,
            self.index + 1,
        )

    def __lt__(self, other):
        return self.start() <= other.start()


class Solution:
    def employeeFreeTime(self, schedule: "[[Interval]]") -> "[Interval]":
        minq = [EmployeeWork(times, 0) for times in schedule]
        heapify(minq)

        freetime_list = []
        while minq:
            work = pop(minq)
            if work.has_next():
                # work's next can be its consecutive interval
                push(minq, work.next())

            if not minq:
                # There isn't a next work interval
                break

            top_work = pop(minq)
            if work.end() < top_work.start():
                freetime_list.append(Interval(work.end(), top_work.start()))
                # work and top_work do not overlap, done with work.
                # Push back top_work
                push(minq, top_work)
                continue

            # work and top_work overlap, merge them.
            merged_work = Interval(work.start(), max(work.end(), top_work.end()))
            push(minq, EmployeeWork([merged_work], 0))

            # top_work is now in merged_work, move to its next
            if top_work.has_next():
                push(minq, top_work.next())

        return freetime_list

unreasonably effective