unreasonably effective

you can be sloppy, as long as you are rigorous

LeetCode 295: Find Median from Data Stream

link

Median is the middle point in sorted order.

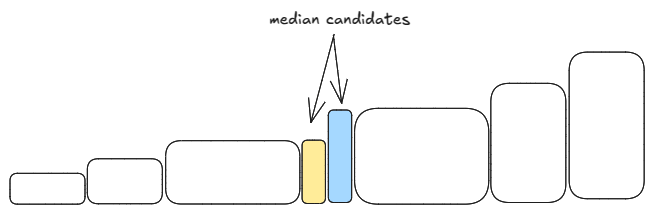
So, we keep track of the middle point by keeping left and right halves of the values in two heaps: (1) max heap for the left half (2) min heap for the right half. So, the tops of these two heaps determine the median at all times.

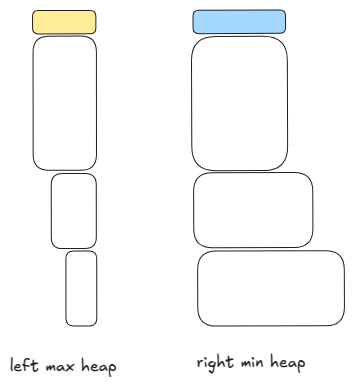
Between the heaps we maintain the two invariants:

  1. \texttt{left-max-heap}_{\text{top}} \le \texttt{right-min-heap}_{\text{top}}.
    • Insert num in the correct heap comparing it against top
  2. 0 \le \texttt{len}({\text{left-max-heap}}) - \texttt{len}({\text{right-min-heap}}) \le 1.
    • Fix length of the two heaps
OperationTimeSpace
__init__\mathcal{O}(1)\mathcal{O}(1)
addNum\mathcal{O}(\lg{n})\mathcal{O}(1)
findMedian\mathcal{O}(1)\mathcal{O}(1)
from heapq import heappush as push, heappop as pop


class MedianFinder:

    def __init__(self):
        self.left_maxq, self.right_minq = [], []

    def addNum(self, num: int) -> None:
        if not self.left_maxq or num <= -self.left_maxq[0]:
            push(self.left_maxq, -num)
        else:
            push(self.right_minq, num)

        if len(self.left_maxq) < len(self.right_minq):
            push(self.left_maxq, -pop(self.right_minq))
        elif len(self.left_maxq) - len(self.right_minq) > 1:
            push(self.right_minq, -pop(self.left_maxq))

    def findMedian(self) -> float:
        if len(self.left_maxq) > len(self.right_minq):
            return -self.left_maxq[0]
        else:
            return 0.5 * (-self.left_maxq[0] + self.right_minq[0])


# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()

Follow up:

If all integer numbers from the stream are in the range [0, 100], how would you optimize your solution?

Since num can have only about hundred distinct values, we can keep these distinct values in the heaps — making push and pop constant time operations. However, len(heap) would not give the actual count of numbers in a half. We need to maintain the actual total sizes of the heaps alongside the frequency of each distinct value.

OperationTimeSpace
__init__\mathcal{O}(1)\mathcal{O}(1)
addNum\mathcal{O}(1)\mathcal{O}(1)
findMedian\mathcal{O}(1)\mathcal{O}(1)
from heapq import heappush as push, heappop as pop

class Heap:
    def __init__(self, is_max_heap):
        self.size = 0
        self.map = {}
        self.heap = []
        self.is_max_heap = is_max_heap

    def push(self, num):
        self.size += 1
        if num not in self.map:
            self.map[num] = 1
        else:
            self.map[num] += 1

        if self.map[num] == 1:
            push(self.heap, -num if self.is_max_heap else num)

    def pop(self):
        top = -self.heap[0] if self.is_max_heap else self.heap[0]
        self.size -= 1
        self.map[top] -= 1
        if self.map[top] == 0:
            del self.map[top]
            pop(self.heap)

        return top

    def top(self):
        return -self.heap[0] if self.is_max_heap else self.heap[0]

    def __bool__(self):
        return self.size > 0

    def __len__(self):
        return self.size

class MedianFinder:

    def __init__(self):
        self.left_heap = Heap(is_max_heap=True)
        self.right_heap = Heap(is_max_heap=False)

    def addNum(self, num: int) -> None:
        if not self.left_heap or num <= self.left_heap.top():
            self.left_heap.push(num)
        else:
            self.right_heap.push(num)

        if len(self.left_heap) < len(self.right_heap):
            self.left_heap.push( self.right_heap.pop() )
        elif len(self.left_heap) - len(self.right_heap) > 1:
            self.right_heap.push( self.left_heap.pop() )

    def findMedian(self) -> float:
        if len(self.left_heap) > len(self.right_heap):
            return self.left_heap.top()
        else:
            return 0.5 * (self.left_heap.top() + self.right_heap.top())


# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()

If 99% of all integer numbers from the stream are in the range [0, 100], how would you optimize your solution?

The distribution looks like below:

We can keep three heaps per half:

  1. left_tail_heap: Regular heap containing num < 0
  2. heap: Distinct value heap containing 0 <= num <= 100
  3. right_tail_heap: Regular heap containing num > 100

For left half, the pop() and top() should poll in the sequence: right_tail_heap, then heap, then left_tail_heap. For right half, the sequence is reversed.

In that way, majority of the time the heap push/pop will be constant time operations.

from heapq import heappush as push, heappop as pop


class Heap:
    def __init__(self, is_max_heap):
        self.size = 0
        self.map = {}
        self.left_tail_heap, self.heap, self.right_tail_heap = [], [], []
        self.is_max_heap = is_max_heap

    def push(self, num):
        self.size += 1

        if num < 0:
            push(self.left_tail_heap, -num if self.is_max_heap else num)
        elif 0 <= num <= 100:
            if num not in self.map:
                self.map[num] = 1
            else:
                self.map[num] += 1

            if self.map[num] == 1:
                push(self.heap, -num if self.is_max_heap else num)
        else:
            push(self.right_tail_heap, -num if self.is_max_heap else num)

    def pop(self):
        self.size -= 1

        if self.is_max_heap:
            if self.right_tail_heap:
                return -pop(self.right_tail_heap)
            elif self.heap:
                top = -self.heap[0]
                self.map[top] -= 1
                if self.map[top] == 0:
                    del self.map[top]
                    pop(self.heap)
                return top
            else:
                return -pop(self.left_tail_heap)
        else:
            if self.left_tail_heap:
                return pop(self.left_tail_heap)
            elif self.heap:
                top = self.heap[0]
                self.map[top] -= 1
                if self.map[top] == 0:
                    del self.map[top]
                    pop(self.heap)
                return top
            else:
                return pop(self.right_tail_heap)

    def top(self):
        if self.is_max_heap:
            if self.right_tail_heap:
                return -self.right_tail_heap[0]
            elif self.heap:
                return -self.heap[0]
            else:
                return -self.left_tail_heap[0]
        else:
            if self.left_tail_heap:
                return self.left_tail_heap[0]
            elif self.heap:
                return self.heap[0]
            else:
                return self.right_tail_heap[0]

    def __bool__(self):
        return self.size > 0

    def __len__(self):
        return self.size


class MedianFinder:

    def __init__(self):
        self.left_heap = Heap(is_max_heap=True)
        self.right_heap = Heap(is_max_heap=False)

    def addNum(self, num: int) -> None:
        if not self.left_heap or num <= self.left_heap.top():
            self.left_heap.push(num)
        else:
            self.right_heap.push(num)

        if len(self.left_heap) < len(self.right_heap):
            self.left_heap.push(self.right_heap.pop())
        elif len(self.left_heap) - len(self.right_heap) > 1:
            self.right_heap.push(self.left_heap.pop())

    def findMedian(self) -> float:
        if len(self.left_heap) > len(self.right_heap):
            return self.left_heap.top()
        else:
            return 0.5 * (self.left_heap.top() + self.right_heap.top())


# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()

tanvirdotzaman

,

Leave a comment