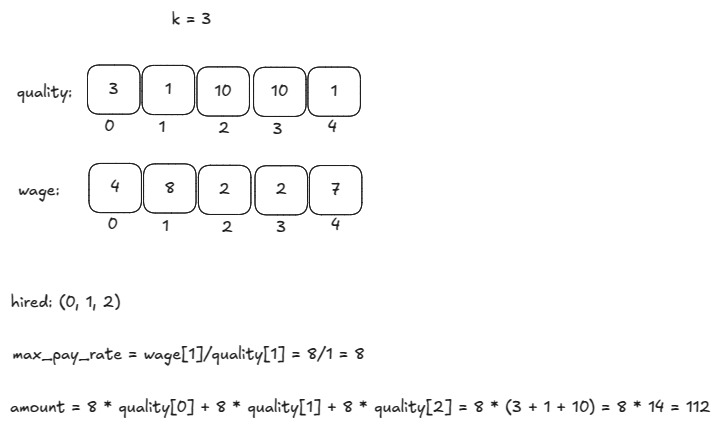
LeetCode 857: Minimum Cost to Hire K Workers

link

If we hire a group of k workers, each worker must be paid at the maximum pay-rate where pay-rate is $\frac{ \text{wage} }{ \text{quality} }$ .

Backtrack

We can try all k-subsets of workers to find the minimum cost.

Time: $\mathcal{O}(n^k \cdot k)$ , space: $\mathcal{O}(k)$ .

class Solution:
    def amount(self, hired, quality, wage):
        wage_rate = max( wage[i]/quality[i] for i in hired )
        return wage_rate * sum(quality[i] for i in hired)

    def backtrack(self, quality, wage, k, hired):
        if len(hired) == k:
            return self.amount(hired, quality, wage)
        
        min_amount = float("inf")
        for i in range(len(quality)):
            if i in hired:
                continue
            hired.add(i)
            amount = self.backtrack(quality, wage, k, hired)
            min_amount = min(min_amount, amount)
            hired.remove(i)
        
        return min_amount
            

    def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:
        return self.backtrack(quality, wage, k, set())

Sort and top-k

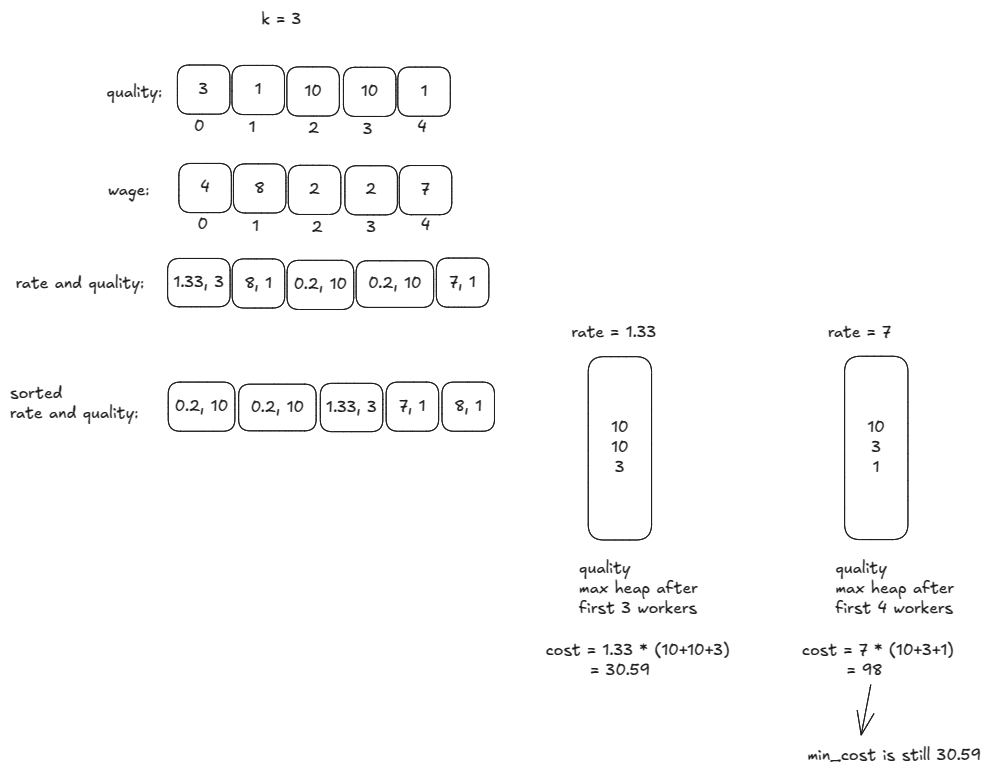
Cost is a product of max-rate and sum-of-qualities. If we did not have max-rate, we could use the k-smallest qualities to form the hired group. Since we need to use max-rate, while finding k-smallest qualities, we process the qualities in non-decreasing order of rates (wage/quality). In that way, if we decide to hire the current worker, we know we need to use that person’s rate as the group rate.

Time: $\mathcal{O}(n \cdot \lg{n})$ , space: $\mathcal{O}(k)$ .

from heapq import heappush as push, heappop as pop

class Solution:
    def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:
        rate_and_quality = [(wage[i]/quality[i], quality[i]) for i in range(len(quality))]
        min_cost = float("inf")
        group_quality = 0
        max_heap = []
        for rate, q in sorted(rate_and_quality):
            push(max_heap, -q)
            group_quality += q
            if len(max_heap) > k:
                group_quality += pop(max_heap)
            if len(max_heap) == k:
                min_cost = min(min_cost, rate * group_quality)
        
        return min_cost

unreasonably effective