LeetCode 542: 01 Matrix

Dynamic programming

For a one-cell (i, j) we can reach the nearest zero-cell via one of its four neighbors. So, if the four neighbors of the cell have already been solved, we can solve (i, j). This suggests DP.

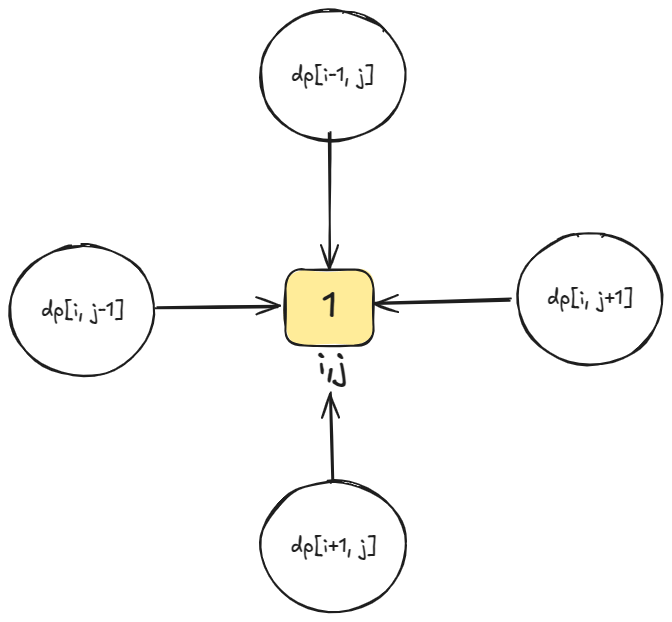
Sub-problem

$dp[i][j] = \begin{cases} 0, & \text{if } mat[i][j] = 0 \\ 1 + \min \left( \left\{ dp[i-1][j], dp[i, j+1], dp[i+1][j], dp[i][j-1] \right\} \right), & \text{otherwise} \end{cases}$

Order

The directed graph has cycles between neighbors.

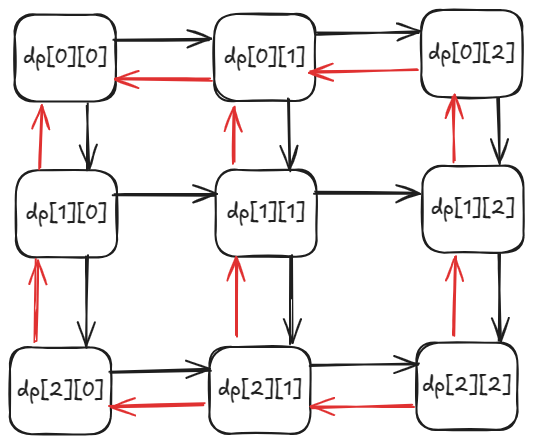
We can process black arrows in one-pass (top-to-bottom, south-east-wards) and red arrows in a second pass (bottom-to-top, north-west-wards). In that way, each pass would have its DAG and would allow topological order.

Time: $\mathcal{O}(m \cdot n)$ . Space: $\mathcal{O}(m \cdot n)$ .

class Solution:
    def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
        m, n = len(mat), len(mat[0])
        dp = [
            [float('inf')] * n for _ in range(m)
        ]
        # Top to bottom
        # South-east wards
        for r in range(m):
            for c in range(n):
                if mat[r][c] == 0:
                    dp[r][c] = 0
                    continue
                up =   dp[r-1][c  ] if r > 0 else float('inf')
                left = dp[r  ][c-1] if c > 0 else float('inf')
                dp[r][c] = min( dp[r][c], 1+up, 1+left )
        
        # Bottom to top
        # North-west wards
        for r in range(m-1, -1, -1):
            for c in range(n-1, -1, -1):
                if mat[r][c] == 0:
                    continue
                down =  dp[r+1][c  ] if r < m-1 else float('inf')
                right = dp[r  ][c+1] if c < n-1 else float('inf')
                dp[r][c] = min( dp[r][c], 1+down, 1+right )
        
        return dp

unreasonably effective