LeetCode 236: Lowest Common Ancestor of a Binary Tree

Recursive

Between the two paths: (1) p -> root and (2) q -> root, the LCA -> root subpath is common. So, if the two paths have different lengths, the difference is in the prefix up to LCA. We can use two pointers to traverse the two paths such that they reach LCA at the same time.

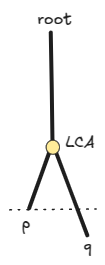
For the longer path, we start ahead by the difference in path lengths.

Time: $\mathcal{O}(n)$ , space: $\mathcal{O}(n)$ .

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def get_path(self, root, u, curr_path):
        if not root:
            return None

        curr_path.append(root)
        if root == u:
            return curr_path[::-1]

        if root.left and (path := self.get_path(root.left, u, curr_path)):
            return path
        if root.right and (path := self.get_path(root.right, u, curr_path)):
            return path
            
        curr_path.pop()
        

    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
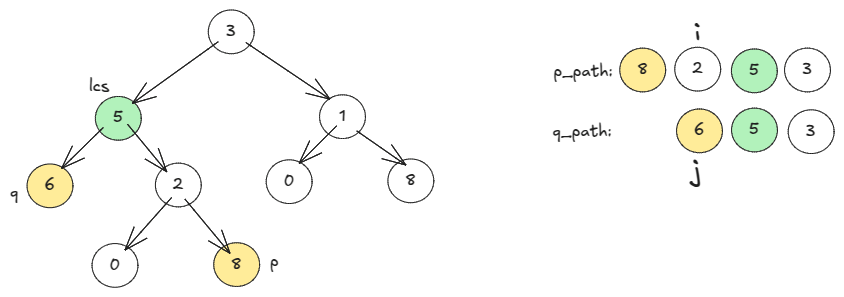
        p_path = self.get_path(root, p, [])
        q_path = self.get_path(root, q, [])
        long, short = (p_path, q_path) if len(p_path) >= len(q_path) else (q_path, p_path)
        i, j = len(long)-len(short), 0
        # First match is lcs
        while long[i] != short[j]:
            i += 1
            j += 1
        return long[i]

Bottom up, LCA is the first node where (found_p, found_q) = (True, True). So, we can traverse the tree once to find the LCA.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:

    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        def find_lca(u, p, q):
            if not u:
                return None, False, False

            lca, left_found_p, left_found_q = find_lca(u.left, p, q)
            if lca:
                return lca, True, True
            lca, right_found_p, right_found_q = find_lca(u.right, p, q)
            if lca:
                return lca, True, True

            found_p = left_found_p or right_found_p or u == p
            found_q = left_found_q or right_found_q or u == q
            lca = u if found_p and found_q else None
            
            return lca, found_p, found_q
            
        
        lca, *_ = find_lca(root, p, q)
        return lca

Iterative

We simulate (found_p, found_q) based bottom up recursion using an explicit stack, visited set, and node_eval dict. Second time we visit a node, on the return path, the evaluation of its children is available. As soon as we find (found_p, found_q) = (True, True) we return the node.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:

    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        visited = set()
        node_eval = {}
        stack = [root]
        while stack:
            u = stack.pop()
            if u not in visited:
                visited.add(u)
                stack.extend(v for v in (u, u.left, u.right) if v)
                continue
            # Return path: (found_p, found_q) evaluation of u's children are available
            left_found_p, left_found_q = node_eval.get(u.left, (False, False))
            right_found_p, right_found_q = node_eval.get(u.right, (False, False))
            found_p = left_found_p or right_found_p or u == p
            found_q = left_found_q or right_found_q or u == q
            if found_p and found_q:
                return u
            node_eval[u] = (found_p, found_q)

        return None

unreasonably effective